Kilogram: Mass and Planck's Constant

Max Planck (1858–1947) originally had no idea how widely applicable his notion of the "quantum" would become, including its role in measuring mass. He conceived it in the context of a stubborn problem in 19th-century physics: A leading theory of the day nonsensically predicted that certain objects would radiate an infinite amount of power when they released electromagnetic radiation at high frequencies (and thus short wavelengths, that is, toward the ultraviolet part of the spectrum in the graph below) — a situation that became known as the "ultraviolet catastrophe."

Planck postulated that electromagnetic energy at a given frequency could only be emitted in discrete amounts, or quanta, whose energy is proportional to h, now known as the Planck constant.

 

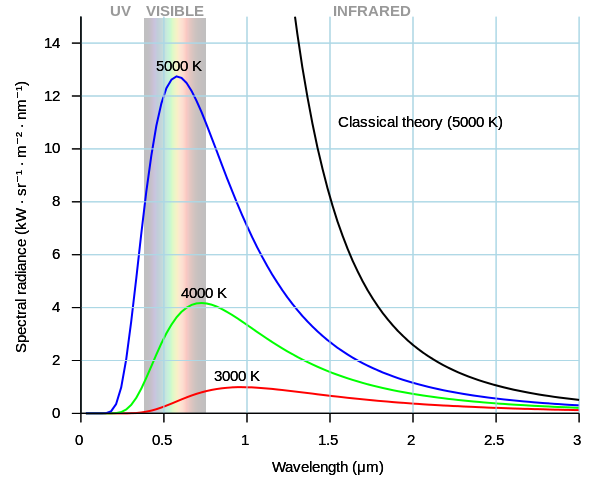
The image above shows what classical theory (the black line) predicted compared to the blue, green and red lines derived from Planck's formulation, which are in excellent agreement with physical measurements.

Mass, Planck and Einstein

How could the SI kilogram unit — embodied in a single lump of metal cast in the 19th century — be redefined in terms of an invariant of nature and scaled up or down conveniently, accurately and repeatedly?

 

After decades of debate, the international measurement science community has chosen to answer that question by using Planck’s constant. 

For many observers, the connection between mass on the scale of a liter of water and a constant deriving from the very earliest days of quantum mechanics may not be immediately obvious. The scientific context for that connection is suggested by a deep underlying relationship between two of the most celebrated formulations in physics.

One is Einstein's famous E =mc², where E is energy, m is mass and c is the speed of light. The other expression, less well known to the general public but fundamental to modern science, is E = hν, the first "quantum" expression in history, stated by Max Planck in 1900. Here, E is energy, ν is frequency (the ν is not a “v” but instead the lowercase Greek letter nu), and h is what is now known as the Planck constant.

Einstein's equation reveals that mass can be understood and even quantified in terms of energy. Planck's equation shows that energy, in turn, can be calculated in terms of the frequency ν of some entity such as a photon (a particle of light), or alternatively, with some mathematical substitutions, a mass — times a multiple of h. The multiple must be a positive integer — such as 1, 2 or 3. The integer aspect is what makes the relationship "quantized" — matter releases energy in discrete chunks, known as “quanta,” which can be imagined as individual packets or bundles of energy.

 

NIST in 90: Measuring Planck’s Constant

Taking the two equations together yields a counterintuitive but hugely valuable insight: Mass — even on the scale of everyday objects — is inherently related to h, which Planck first used to describe the vanishingly small energy content of individual photons emitted by the atoms in hot objects. The value of h is about 0.6 trillionths of a trillionth of a billionth of 1 joule-second. The joule is the SI unit of energy.

As a practical matter, experiments linking mass to h with extraordinary precision became possible in the late 20th century as the result of two separate discoveries that led to two different physical constants related to voltage and resistance, respectively.

These are the Josephson constant (K_J = 2e/h) and the von Klitzing constant (R_K = h/e²).

The Josephson constant is related to the AC Josephson effect. This occurs when a voltage applied across a superconducting junction creates alternating electric current with a frequency that is proportional to the voltage. Frequency can be measured more precisely than any other quantity (something that’s regularly exploited by atomic clocks, which lock onto the microwave or optical frequencies of electromagnetic radiation emitted by atoms).  K_J provides an extremely accurate way of measuring voltage. 

The von Klitzing constant R_K describes the way electrical resistance exists in discrete, quantized values (instead of continuous ones) in certain kinds of physical systems. Because of its extraordinarily high precision, R_K is employed around the world as a standard of electrical resistance. 

Balances or Spheres?

In the 1990s, debate was intensifying about possible ways to redefine the kilogram that would allow for the elimination of the artifact standard. Two principal schools of thought emerged. One would define the kilogram in terms of the mass of a silicon atom by counting the number of atoms in a 1 kg sphere of ultra-pure silicon-28 (the most abundant isotope of silicon, which contains a total of 28 protons and neutrons). 

The other was championed, among others, by NIST scientists Peter Mohr and Barry Taylor. In 1999, in a letter published in the journal Metrologia, they proposed assigning a fixed value to the Planck constant as the basis for a new kilogram definition. Mohr and Taylor explored the use of a Kibble balance, a complex device that measures mass precisely through the use of electrical measurements. 

Named after British physicist Bryan Kibble, the Kibble balance was first developed in 1975 at the UK's National Physical Laboratory (NPL). One was built shortly thereafter at NIST. By the 1980s, scientists at NPL and NIST were heavily involved in using Kibble balances to determine the value of h.

Mohr and Taylor reasoned that if a Kibble balance could use an exactly defined mass to measure the unknown value of h, then the process could be reversed: By setting an exact fixed value of h, the same system could be used to measure an unknown mass.

The idea, which came to be known as the "electric" or "electronic" kilogram, was widely discussed and finally endorsed in principle by the international General Conference on Weights and Measures (CGPM), with a few requirements. At least three experiments must produce measurements with a relative standard uncertainty of no more than 50 parts per billion, with at least one of those measurements having an uncertainty of no more than 20 parts per billion. All these values must agree within a statistical confidence level of 95 percent.

In mid-2017, the international scientific community rose to the challenge and succeeded in  meeting these requirements.

 

Upward of half a dozen Kibble balances are in operation around the world. NIST's final h measurement submitted for the redefined SI had an uncertainty of 13 parts in a billion. Another Kibble balance measurement, from the National Research Council (NRC) of Canada, had an uncertainty of just 9.1 parts per billion. (The NRC had received a Kibble balance from NPL in 2009.) Two other Kibble balance measurements, including one from the LNE (Laboratoire National de Métrologie et d’Essais in France), had the required levels of accuracy. Four measurements from the Avogadro “silicon sphere” also met the international requirements, including three from the multinational IAC (International Avogadro Coordination) and one from the NMIJ (National Metrology Institute of Japan). 

When analyzed by the CODATA Task Group on Fundamental Constants, the measurements produced a final value of h of 6.62607015 × 10^-34 kg⋅m²/s, with an uncertainty of 10 parts per billion. When the SI was redefined, this was set as the exact value of Planck’s constant, which in turn defines other SI units including the kilogram.