Kelvin: Boltzmann Constant

The Boltzmann constant (k_B) relates temperature to energy. It is an indispensable tool in thermodynamics, the study of heat and its relationship to other types of energy. It’s named for Austrian physicist Ludwig Boltzmann (1844–1906), one of the pioneers of statistical mechanics. Statistical mechanics expands upon classical Newtonian mechanics to describe how the group behavior of large collections of objects emerges from the microscopic properties of each individual object.

Newton’s laws govern forces, masses and motions of objects or systems of objects. Newton’s laws are said to be deterministic: That is, someone who has a complete knowledge of the initial conditions of all the objects in a system can predict the future of the system accurately. That is how space missions can place robot landers at specific desired locations hundreds of millions of kilometers from Earth. It’s the same principle that allows expert billiards players to regularly win games.

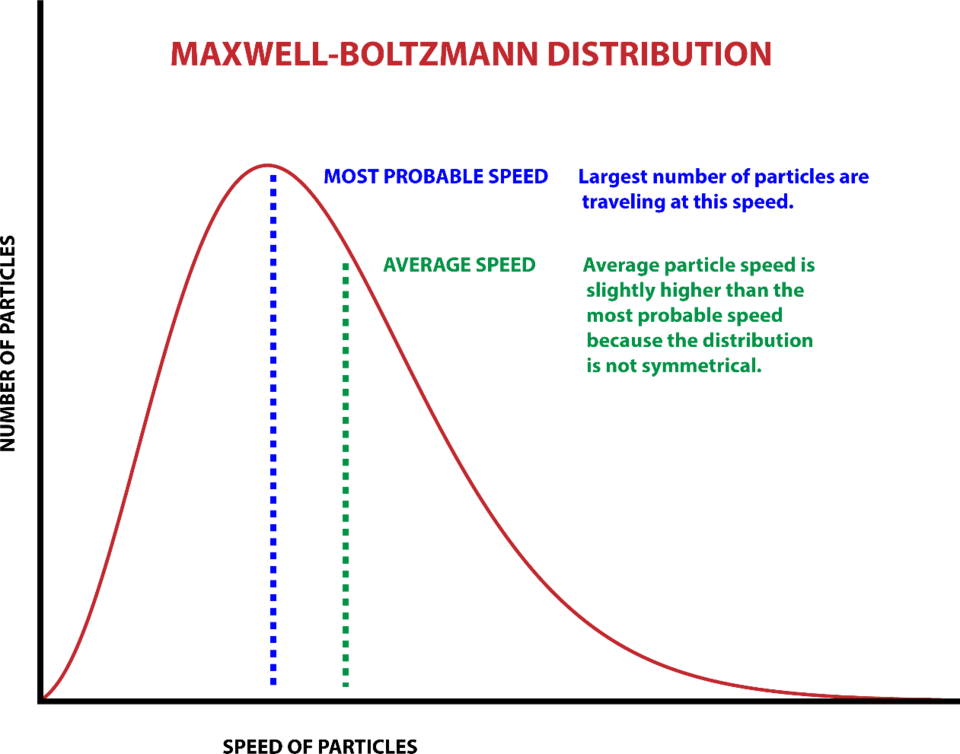
But for a huge ensemble of objects, such as the billions of trillions of hot molecules propelling a piston in a steam engine (the dominant technology of Boltzmann’s era), there is no possible way to determine the state of each independent molecule: They are moving at different velocities with a range of different energies.

For example, air molecules at a room temperature of 25 degrees Celsius (300 kelvins, or 77 degrees Fahrenheit) are traveling at an average speed of about 500 meters per second (1,100 mph). But some are moving at 223 m/s, some at 717 m/s, and so forth, and they are all moving in different directions. Each individual property cannot be known.

Nonetheless, understanding the physics of heat engines and analogous systems demands some way to make mathematically useful statements about collections of enormous numbers of objects. Boltzmann and other scientists showed that it can be done in terms of statistics and probabilities — statistical mechanics. The collective thermodynamic properties of ensembles derive from the sum of the energies of each individual object. Interestingly, different energy values have different probabilities of occurring. 

So how can the average energy content of a gas be calculated? Its energy is proportional to its thermodynamic temperature, and the Boltzmann constant defines what that proportion is: The total kinetic energy (E) in joules is related to temperature (T) in kelvins according to the equation E = k_BT. For scale, 1 joule is the amount of energy expended by a 100-watt light bulb in 0.01 second, or a 1-watt bulb in 1 second.

The Boltzmann constant is thus expressed in joules per kelvin. In November 2018, when the kelvin was redefined, the Boltzmann constant was given an exact fixed value in joules per kelvin. To achieve this redefinition, the following conditions were met: (1) the value obtained by at least one measurement method for k_B had an uncertainty less than 1 part in a million; and (2) at least one fundamentally different type of measurement yielded similar values with uncertainties less than 3 parts per million.

To date, the most accurate values of k_B have been obtained by acoustic thermometry, which relies on the fact that the speed of sound in a gas is directly dependent on its temperature. NIST has a long history of making accurate measurements of the Boltzmann constant with this method. 

Another leading technique is known as dielectric-constant gas thermometry (DCGT), in which researchers measure changes in a gas’s ability to respond to an electric field, known as its dielectric constant. The dielectric constant can depend sensitively on temperature and lead to accurate measurements of the Boltzmann constant. 

NIST and other measurement science institutes are also employing several alternative methods such as Johnson Noise Thermometry (JNT) for measuring the Boltzmann constant. Recent JNT experiments at NIST have yielded a value for k_B with an uncertainty of about 5 parts in a million. Many other new methods have been developed for measuring the Boltzmann constant, including optical measurements of helium gas.

In 2017, the world measurement science community met the requirements for giving the Boltzmann constant an exact value and redefining the kelvin. Acoustic thermometry, DCGT and JNT measurements from various research groups were used in the final determination of the Boltzmann constant for the redefinition of the SI that was  approved in November 2018. Based on these data, the value of k_B in the revised SI is 1.380649 x 10^-23 J K^-1.

While the kelvin was not based on a physical artifact, as the kilogram was for mass, its redefinition is just as momentous. The earlier definition was based on the peculiar properties of a certain isotopic mixture of water, and not directly upon a universal constant of nature. Because it’s not possible to prepare two exactly identical formulations of this mixture, measurements of the kelvin were inevitably slightly different from setup to setup. Basing the kelvin on Boltzmann’s constant puts scientists on the same page, or more precisely on the same letter, k. This enables temperature measurements to be truly universal.