Research Updates – Gas Flow for Semiconductor Manufacturing

13 February, 2025

In our last post in March of 2023, we 1) described design details, 2) illustrated how mass flow is determined, 3) introduced a physical model that characterizes the gas temperature during and after filling the collection tank, $4) compared measured data to the model, and 5) showed tests of repeatability/reproducibility of the rate-of-rise (RoR) gas flow standard.

In this post, we provide details of the first full scale RoR standard, provide validation of the standard, and provide an uncertainty analysis. The information in this update and more can be found in the publication: SLowFlowS: A novel flow standard for semiconductor process gases. https://doi.org/10.1016/j.flowmeasinst.2025.102831

First full scale RoR standard: SLowFlowS

The first full scale semiconductor gas flow standard has been designed and built. We call the semiconductor low-flow standard SLowFlowS. SLowFlowS collection tank as a volume of 2.54 L and consists of 16 tubes connected in series with 1.27 cm outer diameter, 0.127 cm wall thickness, and 1.83 m length each. Therefore, the total length of the tubes, if laid end to end, would be about 30 m. Figure 1 shows SLowFlowS. We installed a ball valve (labelled “small tank valve” in Fig. 1) between the 2nd and 3rd tube of the 16-tube series. Thus, the first two tubes make a 0.32 L tank that we use to collect the smallest flows and to further test our thermal model of the collection tank. We refer to the 16-tube collection tank as the “large” tank and the 2-tube collection tank as the “small” tank. Our thermal model shows that the heat transfer from these long narrow tubes to the ambient air is significantly more effective than the heat transfer from more compact tubes of equal volume. The greater heat transfer facilitates fast thermal equilibration of the gas both during flow and after the flow stops.

SLowFlowS is housed in a temperature enclosure that uses Peltier units to heat and cool. Two fans circulate the conditioned air across SLowFlowS. The spatial difference in the temperature around SLowFlowS is within 100 mK and temporally, less than 2 mK deviations are observed. This along with the tank geometry allows for the gas temperature to be determined within 0.02 % (k = 2).

The first full scale SLowFlowS is a success, however, the FMG is rebuilding the next generation because the long, slender tubes in series in the large tank creates a transient acoustic wave when the collection tank inlet valve closes. Figure 2 shows this transient acoustic wave. The speed of sound of nitrogen is known and we have fast data acquisition that allows us to resolve the wave as it traverses to and from each of the 3 pressure sensors installed as shown in Fig. 1. This makes it impossible to detect the pressure spike we are looking for to measure the temperature of the gas in the collection tank. Therefore, we have redesigned the collection tank so the tubes are in parallel, not series. For the current SLowFlowS, because the geometry is the same in the small tank as in the large tank, we can easily use our small tank to measure pressure spikes and therefore the gas temperature to compare to our model. Equation 3 in our last post shows the temperature rise of the gas away from that of the air in the temperature enclosure is a function of the ratio of mass flow to the length of the tubes. Therefore, we can scale the flow in the small tank to observe the same phenomena as we would in the large tank.

Validation of SLowFlowS

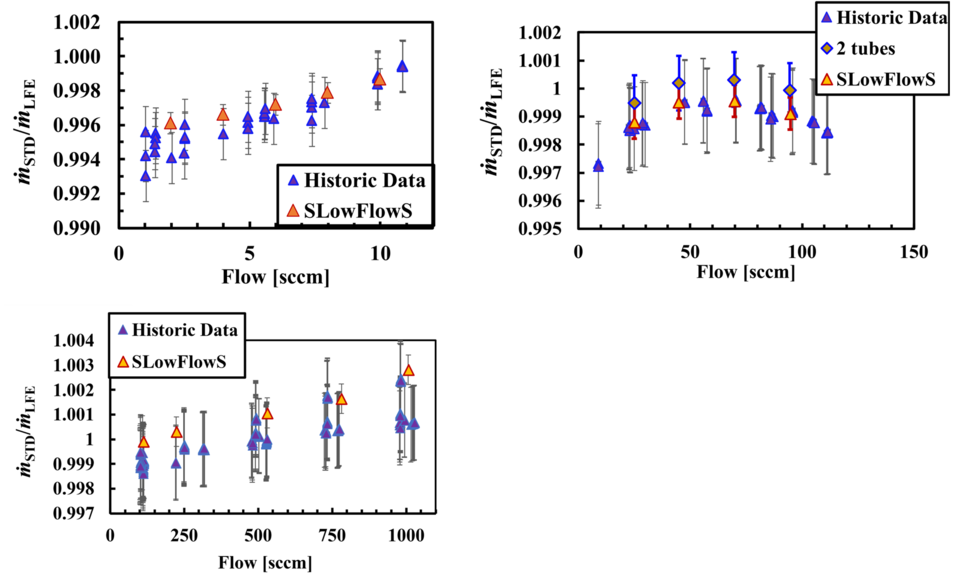
The FMG has validated SLowFlowS using N₂ gas in three NIST working standards and NIST’s primary PVTt gas flow standard. The working standards are laminar flow elements (LFE). The LFEs have an uncertainty of 0.15 % of flow and cover the range of 1 sccm to 1000 sccm (a sccm is a cm³ per minute at 273.15 K and 101.325 kPa). At this time, we do not have a working standard to validate lower flows. Figure 3 shows the results presented as the meter factor, i.e. the ratio of the flow measured by SLowFlowS (ṁ_STD) and the LFE (ṁ_LFE).

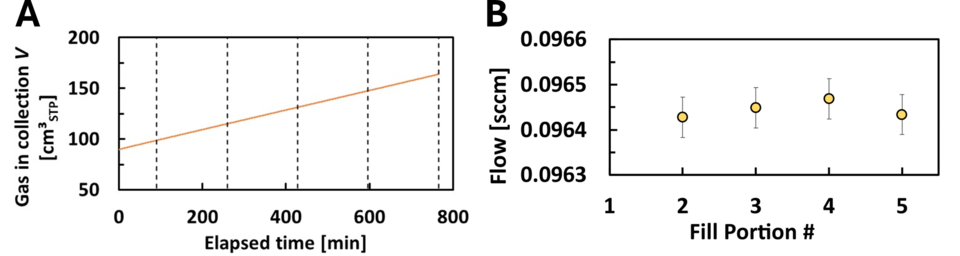
In addition to validating SLowFlowS over the flow range above, we have also tested how well we can maintain a constant flow of 0.1 sccm. To date, we have not achieved our lowest target flow of 0.01 sccm because we lack an upstream pressure regulator for such a low flow. We are currently investigating the availability of a commercial device, or we may make our own as done previously at NIST. We anticipate if SLowFlowS is accurate over the validated flow range, it will be accurate over the lower flows too. This is because there is negligible flow work occurring during these small flows and little to no deviations of the gas temperature from the temperature of the air bath. SLowFlowS has an all-welded collection tank and we have used a helium leak detector to confirm no leaks are observed, therefore, we believe SLowFlowS can accurately measure the lowest of gas flows. To demonstrate this in part, we collected N₂ gas by filling the small collection volume (2 tubes) from approximately 25 kPa to 50 kPa at nominally 0.1 sccm. We broke the fill up into 5 sections, discarding the first section to ensure that we use only the data from the steady portion of the flow as our thermal model predicts. Figure 4A shows the standard volume of gas in the collection tank during the fill. The sections represent a pressure change of approximately 5 kPa each.

This analysis provides enough data to fit a straight line and have the desired uncertainty (k = 2) in the slope of < 0.01 % of the flow. For this data, the expanded error in the slope was at most 8.8×10-7 sccm, which is a fractional uncertainty of 9.2×10-4 %. The results are plotted in Fig. 4B. The vertical bars are the expanded uncertainty in flow for using the small collection tank of SLowFlowS, 0.094 %.

SLowFlowS uncertainty analysis

We determine ṁ during steady-state flow from a linear regression of N discrete values of the density of gas ρ_n in the tank at elapsed times t_n = n Δt, where n = 1, 2, 3, …,  N and Δt is a regular time interval. The density ρ_n is determined from the measured gas pressure P_n, the average temperature T_gas (determined by the procedure in the preceding section), the known equation of state of the gas ρ_n = ρ(T_gas, P_n), and the known volume of the tank V_tank. The value of ṁ from linear regression is

$$\dot{m}=\frac{dM_{\mathrm{tank}}}{dt}=\frac{d\rho}{dt}V_{\mathrm{tank}}=\left(\frac{\sum_{n=1}^{N}{\rho_nt_n}-\frac{1}{N}\sum_{n=1}^{N}{\rho_n\sum_{n=1}^{N}t_n}}{\sum_{n=1}^{N}t_n^2-\frac{1}{N}\left(\sum_{n=1}^{N}t_n\right)^2}\right)V_{\mathrm{tank}}$$

We follow the guidelines for evaluating and expressing uncertainty provided in “Guide to the expression of uncertainty in measurement” (GUM) and Coleman and Steele (Experimentation and Uncertainty Analysis for Engineers. 3rd ed. New York: John Wiley and Sons Inc.; 2009). The combined relative uncertainty of the measured mass flow ṁ is determined using the propagation of uncertainty formula:

$$u^2\left(\dot{m}\right)=\sum_{i=1}^{n}{S_{x_i}^2u^2\left(x_i\right)},$$

where u²(ṁ) is the combined standard uncertainty in ṁ, S_xi = (∂ṁ/∂x_i)x_i/ṁ  is the dimensionless sensitivity coefficient of ṁ on x_i, and u(x_i) is the standard relative uncertainty in x_i. The combined standard relative uncertainty (u_c) is multiplied by the coverage factor (k = 2) to obtain the combined expanded relative uncertainty (U_e).

The uncertainty budget below is for inert gases, which have with a relative standard uncertainty in density of ± 0.01 %. The uncertainty of SLowFlowS will vary with gas density uncertainty. For inert gases, SLowFlowS has an expanded (k = 2) uncertainty (U_e) in the mass flow of 0.056 % if all 16 tubes are used for the collection tank, and 0.094 % if 2 tubes are used. The measured meter factors validating SLowFlowS had a standard deviation of no more than 0.01 %, which means U_e in the meter factor is 0.060 % and 0.096 % for the 16-tube and 2-tube collection tank, respectively.

Table 1 gives the uncertainty components of SLowFlowS. Because the uncertainty in P, T, and V do not change as the collection tank is filled, we use the formula for mass m = ρV to determine the sensitivity coefficients for those variables. The variables in Table 1 are uncorrelated. We fit ρ(t) to a straight line and, therefore, the uncertainty in the fitted slope includes correlations among the ρ(t) values. The fit also includes any uncertainty from timing errors. The computer that runs the data acquisition from SLowFlowS has time traceability to NIST through the NIST internet Time Service. We have observed the clock and updates for numerous simultaneous days and found an asynchronous drift that is a fraction of a microsecond per second. This results in less than a part per million uncertainty in the computer timing, which is insignificant for our purposes. If a significant time synchronization occurs during data collection, we would observe it in the fit residuals of ρ(t) as a discontinuous step. The residuals are observed, and this has not occurred to the best of the FMG’s knowledge.

The largest uncertainty component is the volume of the SLowFlowS collection tank, 0.041 % and 0.086 % of the volume for the large, 16-tube and small, 2-tube collection tank, respectively. These volumes were determined by gas expansion from a cylinder with a volume of 487.285 cm³ ± 0.115 cm³ at 21 °C and 101.325 kPa. The volumes of the 16-tube and 2-tube collection tanks are 2548.72 cm³ ± 0.092 cm³ and 321.90 cm³ ± 0.011 cm³, respectively. As shown in Table 1, this contributes to approximately half of the uncertainty budget. For the smaller, 2-tube tank, this dominates contributing 83 % to the overall uncertainty. The volume determination dominates the uncertainty for the smaller collection tank because the normalized sensitivity coefficients for the variables that determine the SLowFlowS tank volume are inversely proportional to the change in density in the reference volume or in the SLowFlowS collection tank. The density changes are larger when the gas is expanded into the larger, 16-tube collection tank than the smaller, 2-tube collection tank. Therefore, the uncertainty in the collection tank volume gets larger as the tank size gets smaller.

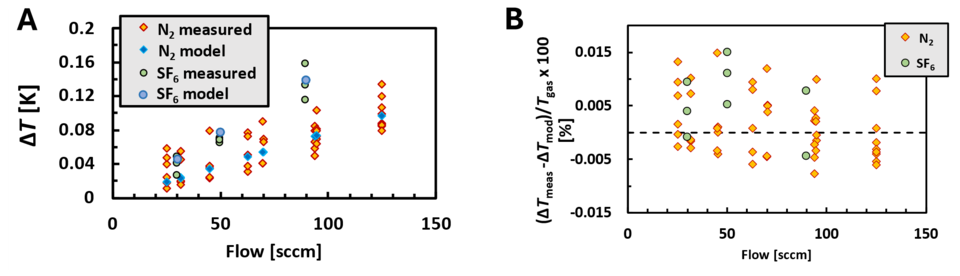
The collection tank has 24 temperature sensors located on it as depicted in Fig. 1C. The uncertainty in the temperature measurement is primarily due to the spatial nonuniformity (38 % contribution to the overall temperature uncertainty) and the way we determine the gas temperature during the filling process (61% contribution to the overall temperature uncertainty). We can measure ΔT as described in the section on determination of mass flow. Figure 5A displays ΔT measured using the small, 2-tube collection tank in the flow range 25 sccm to 125 sccm for nitrogen and sulfur hexafluoride gas. We expect similar results using the large, 16-tube tank for flows between 200 sccm and 1000 sccm (scaled by a factor of 8). The scatter in Fig. 5A resulted from fluctuations in the measured pressure overshoot, likely due to timing issues with the pressure transducer.

The expression in Eqn. 3 from our previous post can be used to calculate ΔT and compare to what we have measured. The computed values are shown by the blue triangles in Fig 5A. In Fig 5B, we calculated the differences between all the measured values and computed values of ΔT and plotted this as a percent of T_gas. The uncertainty in T_gas due to ΔT is determined by these fractional differences. The distribution is between ± 0.015 %. We treat this as a rectangular, or uniform probability distribution and estimate a standard uncertainty of 0.009 % in T_gas.

The remainder of the uncertainty in T_gas comes from the spatial nonuniformity in the temperature enclosure. Our next blog will show our next generation SLowFlowS and updated temperature enclosure.

---

07 March, 2023

NIST’s Rate of Rise Flow Standard (RoRFS)

In our last post, we described the preliminary design of NIST's Rate of Rise Flow Standard (RoRFS) being developed to calibrate semiconductor meters for flows ranging from Q̇ = 0.01 sccm to 1000 sccm at a target expanded uncertainty of 0.1 % or less. This blog 1) provides additional details on the design, 2) illustrates how mass flow is determined, 3) introduces a physical model that characterizes the increase in gas temperature in the collection tank attributed to flow work, 4) compares the measured pressure spike used to determine the temperature with the spike predicted by the physical model, 5) updates the RoRFS collection tank design, and 6) shows tests of the repeatability/reproducibility of a scaled RoRFS using SF₆ and N₂ for flows at approximately 150 sccm.

Design Details

The primary components of the RoRFS are shown in Figure 1 and include 1) the gas source; 2) a mass flow controller (MFC) to establish a constant mass flow; 3) the meter under test (MUT) being calibrated; 4) pressure regulators; 5) a long, slender collection tank of known volume (V_tank); 6) a vacuum pump downstream of the collection tank; 7) pressure and temperature sensors; and 8) valves to start/stop flow and partition the collection tank or other parts of the standard; 9) a thermostatted enclosure (not shown in the figure) that recirculates air at constant temperature T_∞ over the MUT piping and the collection tank.

The design of the collection tank depicted in Fig. 1 illustrates our strategy for limiting flow work related heat transfer effects. Our temperature model discussed later in the blog shows that the long tubing promotes heat transfer, facilitating fast thermal equilibrium of the gas in the tank both during the filling process and after the tank inlet valve is closed and flow stops. Although the schematic in Fig. 1 shows a specific design consisting of N_tubes = 6 finned tubes connected in series, this is not the configuration we have decided to use in our first full size flow standard (we are not sure if it will be the final version at this time). The configuration and design consideration are discussed below in the section about updates to the RoRFS collection tank design. For clarity, experimental results specify these design parameters and provides the tube dimensions D_i and L_tube. The results presented for our bench top standard are with the tubes configured in parallel.

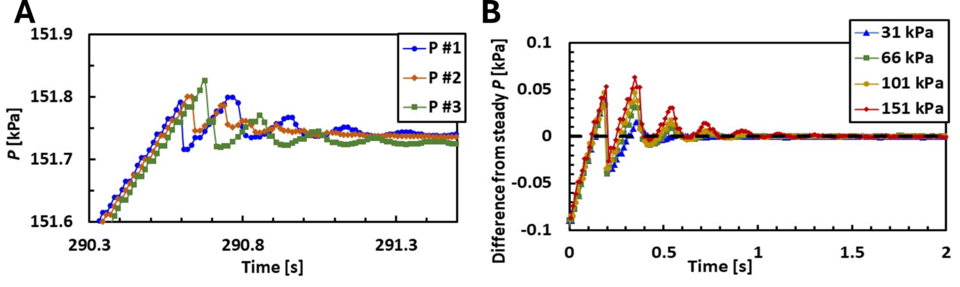
During calibration, the MUT measures the constant mass flow ṁ_MUT established by the MFC. The steady flow exiting the MUT accumulates in the collection tank. A regulator installed immediately downstream of the MUT isolates the MUT from the rising gas pressure in the tank. As the gas enters the collection tank it compresses the existing gas so that the temperature increases during the filling process (i.e., the flow work phenomenon). Accurately measuring this changing temperature with a probe is challenging due to the poor heat transfer between the probe and the nearly stagnant gas. As a result, the RoRFS does not use temperature probes inside in the collection tank. Instead, we measure the temperature T_∞ of thermostatted air outside of the collection vessel and determine the temperature increase ΔT of the gas inside the vessel caused by a balance of flow work and heat lost through the vessel wall to the environment. We determine ΔT by measuring the pressure spike that occurs immediately after the flow is stopped (see Fig. 4). After the flow is stopped, the mass and the average gas density in the collection tank remain constant. Accordingly, changes in pressure correlate with temperature as the temperature relaxes back to T_∞. We exploit this correlation to determine ΔT, and subsequently, the temperature in the collection tank during filling,

How Mass Flow is Determined

Conservation of mass stipulates that the rate of mass accumulation in the collection tank equals the mass flow,

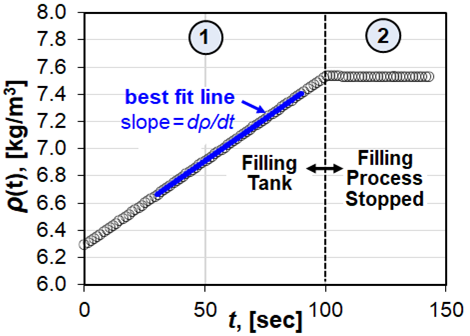
which is equal to the product of the collection tank volume (V_tank) and the rate of change of the density (dρ/dt). Figure 2 shows the increase in the density of SF₆ gas nominally flowing into the collection tank at Q̇ = 163.2 sccm. A NIST traceable equation of state for SF₆ calculates the density ρ = ρ(P, T) at each point (○) as a function of the measured pressure P and the steady state temperature T given in Eq. (1). The rate of change of the density is determined using the slope of the line (──) depicted in Figure 2. Since ρ is determined using the steady state temperature, the slope of the density must be calculated after temperature transients have dissipated when ρ varies linearly with time. We estimate the time required to reach steady state using our temperature model discussed in the next section. In addition, we check that the linear regression of the density versus time data yields an uncertainty of the slope that is no more than 0.01 % at the 95 % confidence level. If the selected data used to compute the slope does not satisfy this criterion, the tank is evacuated, and the filling process is repeated.

Temperature Model

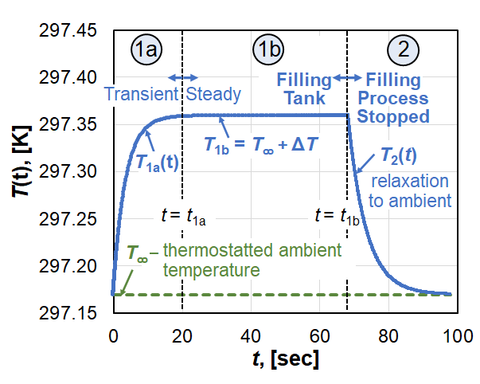
We developed a physical model based on mass and energy conservation to predict the gas temperature in the collection tank throughout the calibration process. This model is important because it tells us when the data is acceptable to calculate the slope of the mass vs. time, i.e., that the temperature has reached the steady state value during filling. The results of the model are illustrated by the two temperature traces shown in Fig. 3. The dashed line (----) shows the constant temperature T_∞ of the thermostatted air outside the collection tank while the solid line (──) shows the gas temperature T inside the tank. These temperature traces are depicted during two periods: 1) the period during flow when mass accumulates in the collection volume, and 2) the period after the flow stops and M_tank is constant. The dashed vertical line (----) at t = t_1a divides the filling period into 2 intervals. The interval t < t_1a shows the transient gas temperature T_1a that increases above T_∞ to the steady state temperature T_1b due to flow work. The slope of the density in Fig. 2 is calculated after the time t_1a predicted by the model. For the interval t ≥ t_1a the heat generated by flow work is balanced by heat loss through the collection tank walls so that T_1b = T_∞ + ΔT is nearly constant. The model predicts the temperature increase due to flow work is

where ṁ is the mass flow, the gas constant R_gas =R_univ/M is the ratio of the universal gas constant and the molar mass of the semiconductor gas; k is the gas thermal conductivity, L_tube is the length of the collection tank tube(s); and N_R is a virial correction parameter that is generally close to unity. Historically, the semiconductor industry expresses mass flow in volumetric units at standard, or reference conditions of P_REF = 101.325 kPa and T_REF = 273.15 K. To accommodate readers familiar with this notation, the mass flow in Eq. (3) is expressed as a standard volumetric flow, ṁ = ρ_REF Q̇. Here, ρ_REF = ρ(P_REF, T_REF) is the density of the gas evaluated at standard pressure and temperature using the REFPROP database.  

We use Eq. (3) to support the design of the collection tank. For example, the gas species dependence of ΔT depends solely on the thermodynamic and transport properties expressed by

$$\frac{N_{R}ρ_{REF}R_{univ}}{(Mk)}$$

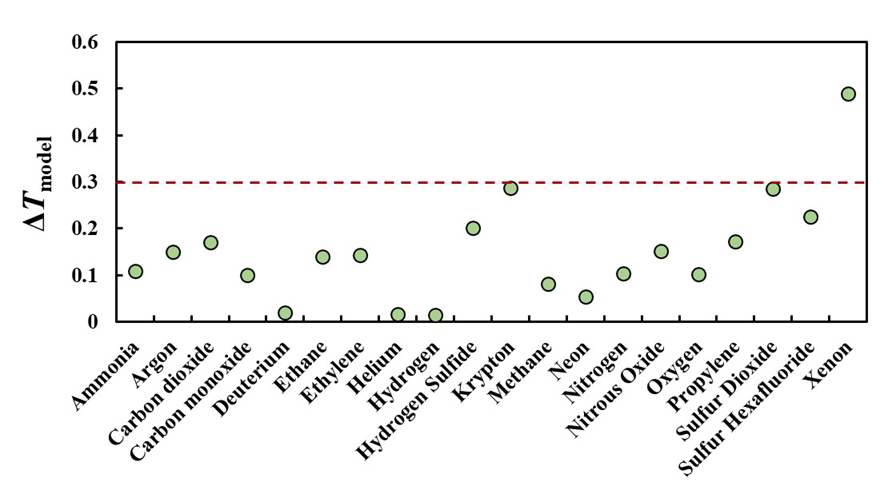
in Eq. (3). For a specified flow Q̇ accumulating in the collection tank consisting of tubes of length L_tube with thermostatted air at T_∞, the temperature increase ΔT depends only on the gas properties of the semiconductor gas. For a given tank volume, one can decrease ΔT by increasing the length L_tube of the tubes comprising the collection tank. Using this strategy, we designed our collection tank so that the maximum temperature increase due to flow work is less than ΔT_max  ≤ 0.3 K for the majority of the gasses we plan to investigate. To realize the desired temperature criterion, we plan to design a collection tank with N_tubes = 16 each having D_i = 0.010 m and L_tube = 1.8 m for a total length of 29.28 m, and the maximum flow is Q̇ = 1000 sccm. Figure 4 shows ΔT for many semiconductor gases. We would need 26 tubes to achieve a 0.3 K change for xenon gas. This would lead to a significantly longer collection time for the other gases and is not seen as a necessity at this time. Note that the uncertainty in the temperature measurement will be much smaller than ΔT: we will measure the pressure spike and apply our physical model to correct for the flow work effects on the temperature measurement.

Comparison of the Model to Experiment

Figure 5 shows some example pressure spikes measured in our benchtop standard. These spikes indicate the measured room temperature is 0.04 % and 0.07 % different from the internal gas temperature during filling for N₂ and SF₆ gas, respectively. This is a correction we can easily make. We tested our model against experimental data for the original planned tube size for our collection volume (D_i = 0.021 m, or 0.825 in) and the revised tube size (D_i = 0.010 m, or 0.3925 in) since the last blog post. L_tube = 1.8 m and the tubes are configured in parallel. Figure 5 shows the results for a flow of ≈ 150 sccm of N₂ and SF₆ in both tube sizes. The model (──) predicts the measured pressure spike (○) within 15 % for our maximum flow of N₂ and SF₆. This corresponds to a maximum expanded uncertainty in the gas T of 0.015 %. The temperature uncertainty will be much lower for smaller flows where the flow work is minimal and ΔT < 0.3 K.

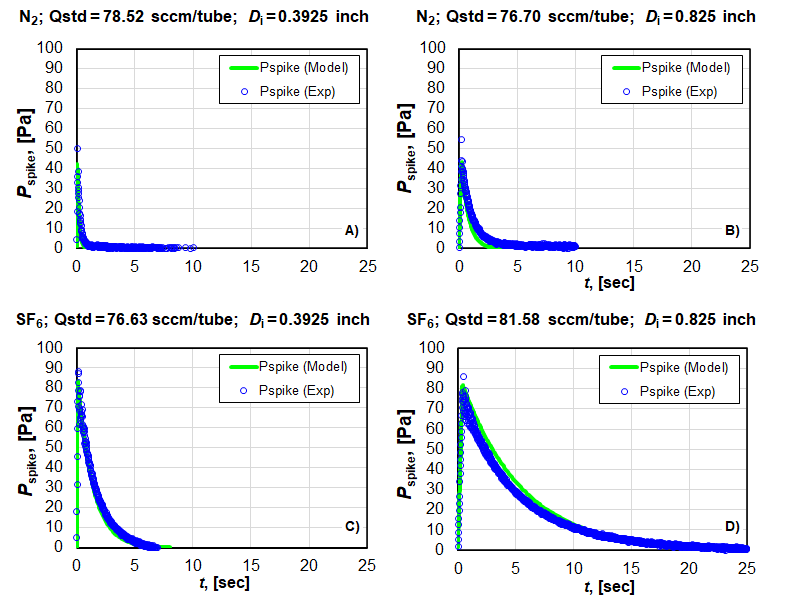
It is important to notice the time it takes to reach thermal equilibrium once the flow is stopped in Fig. 5 for the two different tube diameters. Because the volume of collected gas is less in a tube of the same length but smaller diameter, the time for it to reach equilibrium is less. This is also true with respect to the time it takes to equilibrate when filling begins as discussed above. It is desirable to have the gas reach equilibrium quicker when filling because that allows the collection of more data points to reduce the error in the slope calculation. However, it is also important that the pressure spike is well-resolved in order to make an accurate temperature correction: it may be hard to measure its true magnitude if the response time of the pressure sensor is too low. We have decided to use tubing with a nominal diameter of 1.27 cm (measured D_i = 0.010 m, or 0.3925 in). We believe this is the lower limit to obtain adequate resolution of the pressure spike.   

Updates to the RoRFS Design

Since our last post, the FMG has decided 1) to reduce the size of the collection volume, 2) eliminate the fins on the tubes, and 3) plumb the tubes in series. Modeling of flow work produced while filling the tubes and experimental results show that we do not need the large volume of 15 L originally planned; 2.4 L will provide sufficient filling time. Therefore, we will use tubing with D_i = 0.010 m. We will plumb 16 tubes, each with L_tube = 1.8 m in series to make the final volume of 2.4 L with L = 29.3 m. 

We plumbed two of the smaller diameter tubes together in parallel for a revised benchtop standard with V  ≈ 0.363 L  (Fig. 6) and the data presented below is from that arrangement. Our benchtop standard is a factor of 8 smaller than our planned volume and the maximum scaled flow is 150 sccm. (1000 sccm is our planned maximum flow in the final volume.) Prior testing showed that the fins are not necessary, and we decided to plumb the tubes in series because it is much easier than parallel.

In addition to reducing our collection tank volume, we replaced a pressure sensor that has a response time of ≈ 6.2 Hz with one with a response time of ≈ 52 Hz. This allowed us to better resolve the pressure spike and better determine ΔT, which allowed us to physically model the heat transfer in the tank as discussed above.

We verified our new volume will give us an acceptable amount of data points over the flow range of 1 sccm to 150 sccm. This is important for the fit to the calculated gas density vs. time to determine the gas flow. The pressure and temperature sensors have inherent noise. We need enough data that the fit of a straight line gives acceptable uncertainty. We can achieve 95 % uncertainty in the slope of this line within 0.01 %.

Repeatability/reproducibility of a scaled RoRFS

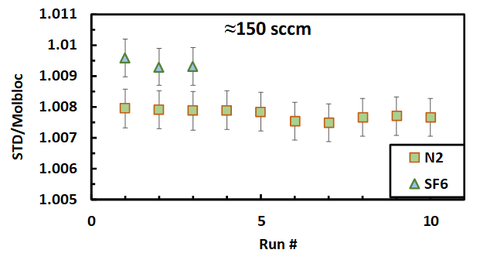
We have begun to validate our benchtop standard using a molbloc and N₂ and SF₆ gas. Figure 7 shows the meter factor, the ratio of the flow determined by the standard to that reported by the meter. We compared repeated rate-of-rise measurements and the molbloc at ≈ 150 sccm. No sensors were calibrated and hence this test only measures the repeatability of our standard. The meter factor, i.e., the flow according to the standard divided by the flow measured by the molbloc is plotted on the y-axis. For N₂, five measurements

were made sequentially. Then the flow was turned off, restarted, and five more measurements were collected, giving a total of ten total measurements. For SF₆, three measurements were made sequentially. The standard deviation of the 10 N₂ meter factor measurements is 0.02 %, which is the same for the 3 SF₆ meter factor measurements. This shows the benchtop RoRFS has repeatability that is more than adequate for our purposes. The error bars are 0.05 % of the meter factor, which is our target k = 2 uncertainty for inert gases with known properties. It should be noted the meter factor is different for the two gas species. This is the reason for undertaking for this work: to measure and model the gas property effects on the flow meters used in chip fabrication 

Our next step is to weld together 16 of the nominal 1.27 cm diameter tubes in series to achieve our final volume. We will then place this volume in a temperature-controlled enclosure. In a future blog we will described the RoRFS thermostated enclosure (still under construction) and describe its effectiveness maintaining constant surface temperature on the outer surface of the collection tank during the calibration process. While the thermal enclosure is being completed, we measure T_∞ by averaging readings from 4 thermistors spaced axially along the length of the collection tank tubing (Fig. 6). Each thermistor measures the air adjacent to the tube wall every 1.5 s throughout the calibration process.

---

08 December, 2022

The Fluid Metrology Group (FMG) has begun the design and construction of a semiconductor gas flow standard. It will use the rate of rise technique, in which the rate of change of gas density in a collection volume measured over time gives the mass flow. Figure 1 shows a prototype for the flow standard, which is approximately an order of magnitude smaller in volume than the target design. We call this our benchtop standard.

We have procured finned tubes as shown in Fig. 1 for a collection volume. The tubes are 1.85 m long and have an outer diameter of 0.0254 m. The original plan was to use 16 of them for a final volume of approximately 15 L. However, final tube size, shape, and number will be determined from our benchtop standard. Our maximum planned flow is 1000 sccm, which is equivalent to 150 sccm when scaled for our smaller benchtop standard. In addition to building a standard to measure semiconductor gas flow, we are working closely with NIST’s Thermophysical Properties of Fluids Group to determine gas properties for gases used in semiconductor manufacturing. The FMG has previously measured properties of some semiconductor gases, which can be found here.

To accurately measure the density as the collection tank is filling, we must be able to measure the incoming gas temperature and pressure with appropriate response time and resolution and have an equation of state to calculate the density from these inputs. Currently, the FMG has a rate of rise gas flow standard for inert gases with well-known equations of state. The collection volume is submerged in a well-stirred, temperature-controlled water bath whose temperature we measure. We do not measure the temperature of the gas in the volume directly. As the collection tank fills, heat generated in the gas by flow work will be balanced by the heat transfer to the water bath, i.e., the gas temperature will rise above that of the water temperature. For low flows, this gas temperature rise is negligible, but as the flow is increased, the gas temperature increase produces an error in the calculated density and must be corrected. This phenomenon produces a “pressure spike” when the flow is stopped as shown in Fig. 2. Because water is corrosive and a large water bath is difficult to maintain, we are testing whether a temperature-controlled air bath will work instead. With sufficient heat transfer, the difference between the temperature of the gas in our full collection volume and the air bath will be insignificant. Alternatively, if the temperature error is predictable, we can make the necessary correction.

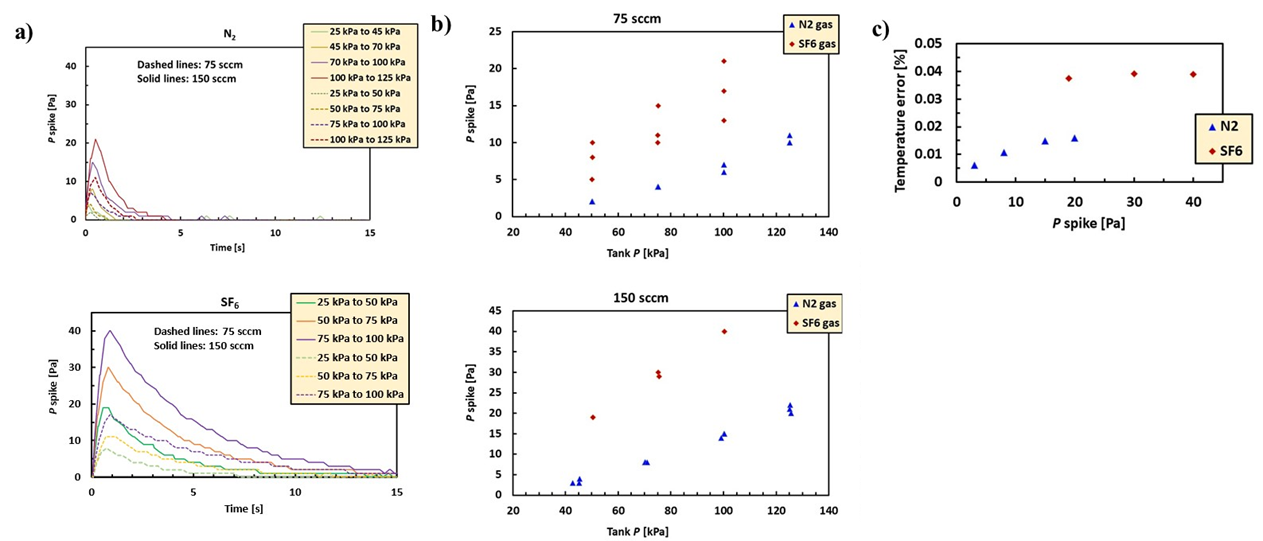
We have measured the magnitude of the pressure spike (and hence the temperature error caused by flow work) in our benchtop standard using nitrogen and sulfur hexafluoride gases with and without air blowing across the finned tubes. We chose these two gases because they have very different heat capacities and thermal conductivities [C_p/C_v = 1.4 for N₂ and 1.1 for SF₆, thermal conductivity = 25.24 mW/(m-K) for N₂ and 12.38 mW/(m-K) for SF₆]. We see no effect on the magnitude of the pressure spike when a large fan is used to flow air across the tubes. This means our heat transfer is limited by the heat transfer inside the collection volume, so now we are investigating designs that improve the internal heat transfer. In a future update, we will discuss some theoretical models that describe the thermodynamics during the filling process that predict the temperature error to guide our design effort.