An official website of the United States government
Here’s how you know
Official websites use .gov
A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.
Figure 1. The hydrogen atom numbering and methane orientation in the molecule-fixed axis system used in this article.
2. Familiar Point Group Ideas
2.1 Geometric operations
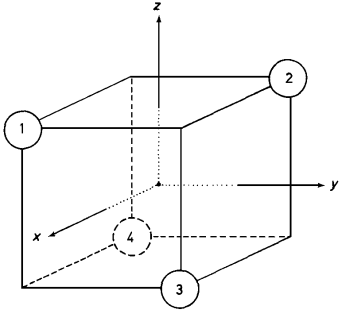
Figure 1 illustrates the four hydrogens of CH4 numbered [17] and placed at the corners of a cube whose faces are perpendicular to the Cartesian axes. At least six other schemes for associating numbered hydrogens with corners of the cube in Fig. 1 occur [5, 9, 18-21]. Examination of Fig. 1 shows it to be invariant (apart from atom numbering) under the following 24 point group operations: the identity; eight three-fold rotations; three two-fold rotations; six four-fold rotation-reflections; and six planar reflections. The point group consisting of these operations is called Td. Its character table [2-4] is given in Table 1.
Table 1. Character table for the point group Td
E
8C3
3C2
6S4
6σd
A1
1
1
1
1
1
αxx + αyy + αzz
A2
1
1
1
-1
-1
E
2
-1
2
0
0
(2αzz - αxx - αyy , αxx - αyy)
F1
3
0
-1
1
-1
R
F2
3
0
-1
-1
1
T
(αyz , αzx , αxy)
The individual operations occurring in this point group for a methane molecule oriented as shown in Fig. 1 will be denoted here by the symbols: E; C3(1,1,1), C32(1,1,1), C3(-1,1,1), C32(-1,1,1), C3(-1,-1,1), C32(-1,-1,1), C3(1,-1,1), C32(1,-1,1); C2(x), C2(y), C2(z); S4(x), S43(x), S4(y), S43(y), S4(z), S43(z); and σd(0,1,1), σd(0,-1,1), σd(1,0,1), σd(1,0,-1), σd(1,1,0), σd(-1,1,0); respectively, where directions of three-fold rotation axes and of perpendiculars to the planes of reflection are specified by three indices representing coefficients of unit vectors along the Cartesian axes x,y,z. One of these geometrical symmetry operations in general will be denoted by P.
