Official websites use .gov
A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.
Computation of Atomic Properties with the Hy-CI Method
Computation of Atomic Properties with the Hy - CI Method
Summary:
Impressive advances have been made throughout the years in the study of atomic structure, at both the experimental and theoretical levels. For atomic hydrogen and other equivalent two-body systems, exact analytical solutions to the nonrelativistic Schroedinger equation are known. It is now possible to calculate essentially exact nonrelativistic energies for helium (He) and other three-body (two-electron) systems as well. Even for properties other than the nonrelativistic energy, the precision of the calculation has been referred to as essentially exact for all practical purposes, i.e., the precision goes well beyond what can be achieved experimentally. These high-precision results for two-electron systems have been produced using wave functions which include interelectronic coordinates, a trademark of the classic Hylleraas (Hy) calculations in the 1920s. The Hy-CI method is a hybrid method which includes interelectronic coordinates in the wave function to mimic the high precision of Hy methods, but also includes configurational terms that are the trademark of the conventional Configuration Interaction (CI) methods employed in calculating energies for many-electron atomic (and molecular) systems.
Additional Technical Details:
Why is the Hy-CI Method Important?
In any attempt to get very precise energies, large basis sets have to be employed, which means that linear dependence in the basis set is never very far away. To proceed to tens of thousands of terms in a wave function, extended precision arithmetic is needed to obviate the linear dependence problem, which in turn leads to higher CPU costs. The use of tens of thousands of terms in a wave function leads to memory problems arising from storage of the matrix elements prior to the matrix diagonalization step. And this is true already for the two-electron case of helium (He) and its isoelectronic ions (He-like systems). Where three electron atomic systems (lithium (Li) and other members of its isoelectronic series) have been treated essentially as accurately as He-like systems, demand on computer resources has increased by 6000 fold. Because of these computational difficulties, until recently in the four electron case (beryllium (Be) and other members of its isoelectronic series) there were no calculations of the ground or excited states with an error of less than 0.1 microhartrees (0.0000001 hartree). The challenge for computational scientists is to extend the phenomenal He accomplishments to three, four, and more electron atomic systems. This is where the Hy-CI method becomes important, because the use of configurations wherever possible leads to less difficult integrals than in a purely Hy method, and if one restricts the wave function to at most a single interelectronic coordinate to the first power, then the most difficult integrals are already dealt with at the four electron level and the calculation retains the precision of Hy techniques, but is greatly simplified.
Applications:
The Hy-CI method has been used to compute not only energy levels, but also other atomic properties such as ionization potentials, electron affinities, electric polarizabilities, and transition probabilities of two, three, and four electron atoms and other members of their isoelectronic sequences. In the early parallel work, Hy-CI method calculations with up to 4648 expansion terms were carried out for the ground 1S state of neutral helium and four of its isoelectronic ions, (H-, Li+, Be+2 and B+3).This has resulted in high-precision results for the nonrelativistic energies that are believed to be accurate to 20 decimal digits. This work employs a very novel wave function, namely, one consisting of at most a single r12 raised to the first power combined with a conventional non-orthogonal configuration interaction (CI) basis. This technique can be extended to multielectron systems (more than three or four electrons). The combination of computational simplicity of this form of the wave function, compared to other wave functions of comparable accuracy, as well as the use of parallel processing and extended precision arithmetic, make it possible to achieve levels of accuracy comparable to what has been achieved for He (a two electron atom), for atoms with more than two electrons.
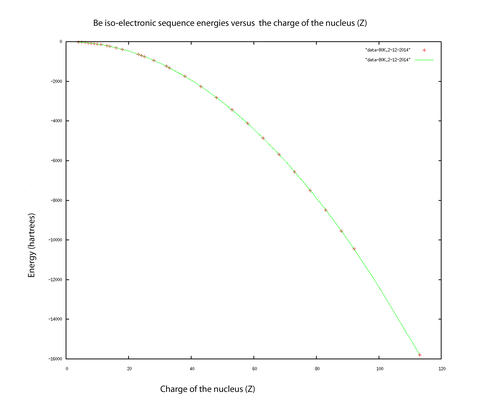
Indeed, the technique has been used to obtain results for the nonrelativistic energies for four excited states of the lithium atom which represented at the time the highest level of accuracy ever reached (10-10 hartree) in atomic quantum computations with more than two electrons. Recent work has included demonstrating what precision can be obtained for atomic beryllium, the key to multielectron (more than four electrons) systems, since the integrals that arise for more than four electrons are of the same type as the ones that arise in the four electron systems. One of our publications discusses the most difficult integral arising in Hy-CI calculations, the three-electron triangle integral. We found that convergence acceleration techniques could be used to speed up the convergence of the integral and hence remove the real bottleneck to highly accurate Hy-CI calculations. Another of our publications tackles making the four electron integrals, the real bottleneck at the four and more electron level, as efficient as possible. The utility of these techniques has been demonstrated in calculations of the nonrelativistic energies of the four electron atomic ground state with nuclear charge ranging from four through 113 (110 states) with record levels of accuracy. (Please refer to figure above).
The figure displays the results of these calculations, where the calculated data points are marked in red and a smooth curve covering the entire isoelectronic sequence is drawn in green. Excited states of atoms have more diffuse electron densities, and Hy-CI was used to calculate the higher, more diffuse Rydberg states with more complicated nodal structures to the same level of precision as the less excited states.
While this work has demonstrated the efficacy of Hy-CI as a solution to the N-body problem for four or more electrons, this work has also shown the presence of a slow convergence problem at the nanohartree precision level which is ultimately built into Hy-CI for four or more electrons. Hy-CI has been generalized to an exponentially correlated Hy-CI (E-Hy-CI) method in which the single linear interelectronic coordinate of an Hy-CI wave function is generalized to a form which pairs an exponential factor with linear interelectronic coordinates, producing a correlation factor which has the right behavior as the interelectronic distance goes to 0, and also as it goes to infinity. The E-Hy-CI wave function expansion method has been used to achieve record levels of precision for not only ground but also excited states of both S and P symmetry of the first row of the He isoelectronic sequence. The wave functions have been used to calculate oscillator strengths, including rigorous quantum mechanical upper and lower bounds, for the resonance transition that are standards of reference for this important atomic property.
This work has extended the accurate calculation of atomic properties from the two-and three-electron level to the four-electron level and has demonstrated that doing really accurate calculations on atoms with the number of electrons greater than or equal to five is a real possibility.
Publications:
High-Precision Hy-CI and E-Hy-CI studies of Atomic and Molecular Properties
Parallel Generalized Real Symmetric-Definite Eigenvalue Problem
Hylleraas-Configuration Interaction study of the singlet S ground state of the negative Li ion
Hylleraas-configuration-interaction Study of the Singlet S Ground State of Neutral Beryllium
Accelerating Scientific Discovery through Computation and Visualization