Moiré Systems

Summary

Moiré quantum matter (MQM) systems consist of stacked and twisted layers of van der Waals materials and have emerged as versatile condensed-matter quantum simulators. The twist angle, choice of material, number of layers, and application of electric and magnetic fields provide a vast playground for realizing quantum phases resulting from the interplay between electron correlations and topology. The discovery of flat electronic bands hosting superconductivity and correlated insulating states in magic-angle twisted bilayer graphene (MATBG) inspired rapid exploration of the parameter space. In this project, we are engineering flat electronic band systems involving graphene heterostructured devices as a platform for condensed-matter quantum simulators. In many cases, the Berry curvature of the electronic bands plays a central role in the physics of the system, which we are studying with Landau level spectroscopy using scanning tunneling microscopy measurements coupled with theoretical computations, as well as combined with electrical transport measurements and atomic force measurements. 

Description

Twisted double bilayer graphene

The moiré systems of magic angle twisted bilayer graphene (MATBG) and related heterostructures support topological bands with nonzero Chern number, which is derived from the Berry curvature of the Bloch wave functions. Berry curvature is intimately related to orbital magnetization, and indeed, previous work on MATBG and related systems has observed orbital magnetic order, valley Hall and quantum anomalous Hall effects. Berry curvature and the related quantum metric also provide significant contributions to the orbital magnetic susceptibility. The valley-contrasting orbital magnetism and orbital magnetic susceptibility play a central role in the material response to applied magnetic fields. Landau level spectroscopy is a well-established tool to experimentally deduce the zero-field properties of the band structure, and in this work, we expand its application to extracting higher-order magnetic response functions in the application to twisted double bilayer graphene (TDBG). 

Figure 1A shows the simulated band structure of TDBG at θ = 1.75° using the Bistritzer–MacDonald (BM) continuum model. The moiré periodic potential leads to narrow moiré mini-bands, composed of two low-energy bands—the valence V1 and conduction C1 bands—and higher remote energy bands—V2 and C2. The narrow bands V1 and C1 have a bandwidth of about 50 meV and are isolated from other bands (Fig. 1B). The TDBG system displays a large tunability in its electronic structure. A perpendicular electric field induces a potential difference between the layers of TDBG, drastically altering the V1 band structure. The V1 band is relatively flat at zero displacement field (Fig. 1B) and develops pronounced electron and hole pockets at D ≠ 0 (see Fig. 1C and fig. S8).

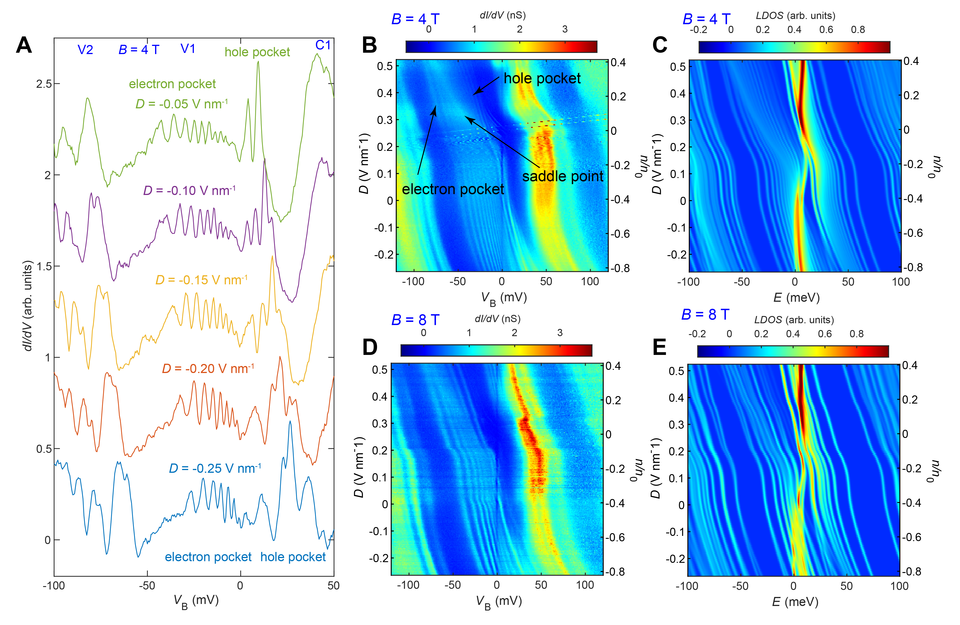
Figure 1E shows the experimental LDOS map of the differential tunneling conductance as a function of sample bias, 𝑉_B, the displacement field D, carrier density 𝑛, and magnetic field, 𝐵 at 𝐵 = 0 T. The low-energy bands V1 and C1 and remote bands V2 and C2 and their evolution with displacement field are clearly visible. The experimental data qualitatively agree with the modeled LDOS of the top layer of the four-layer graphene system using continuum model calculations (Fig. 1F).

Fig. 1. Tuning the narrow electronic bands in TDBG with displacement field at 𝜃 = 1.75°. (A) Energy band structure of TDBG showing the four low-energy bands computed using a continuum model with interlayer potential 𝑈 = 0 meV and 𝜃 = 1.75°. Line cuts from the energy bands in (A) along 𝑘_𝑥 = 0 for (B) 𝑈 = 0 meV and (C) 𝑈 = 80 meV. A dashed horizontal line indicates the position of the Fermi level which moves through the bands as the displacement field and carrier density are varied. (D) STM topographic image of the TDBG moiré pattern, with moiré wavelength 𝜆 = (8.1±0.1) nm. Inset: A magnified portion of the image showing the atomic lattice of graphene. A twist angle of 𝜃 = (1.74° ± 0.02°) was determined from the atomically resolved moiré lattice. The red dot indicates the ABBC symmetry position where the spectral maps with applied magnetic field were acquired. Tunneling setpoint, 𝐼 = 20 pA, 𝑉_B = 100 mV. Temperature T = 0.01 K. (E) Tunneling spectral maps in the D vs. 𝑉_B plane for 𝐵 = 0 T. 𝑛₀ (-𝑛₀) indicates the electron density at full filling of the C1 (V1) band. Setpoints: 𝐼 = 150 pA, 𝑉_B = 120 mV, T = 0.01 K. (F) Corresponding theory map for 𝐵 = 0 T (continuum model calculation). The energy scale in the calculations does not exactly match the experiment, as found in previous calculations; a scaling factor of approximately x1.3 should be applied to the calculations to compare with experiment. Reference, https://www.science.org/doi/10.1126/science.adf2040. 

Credit: NIST

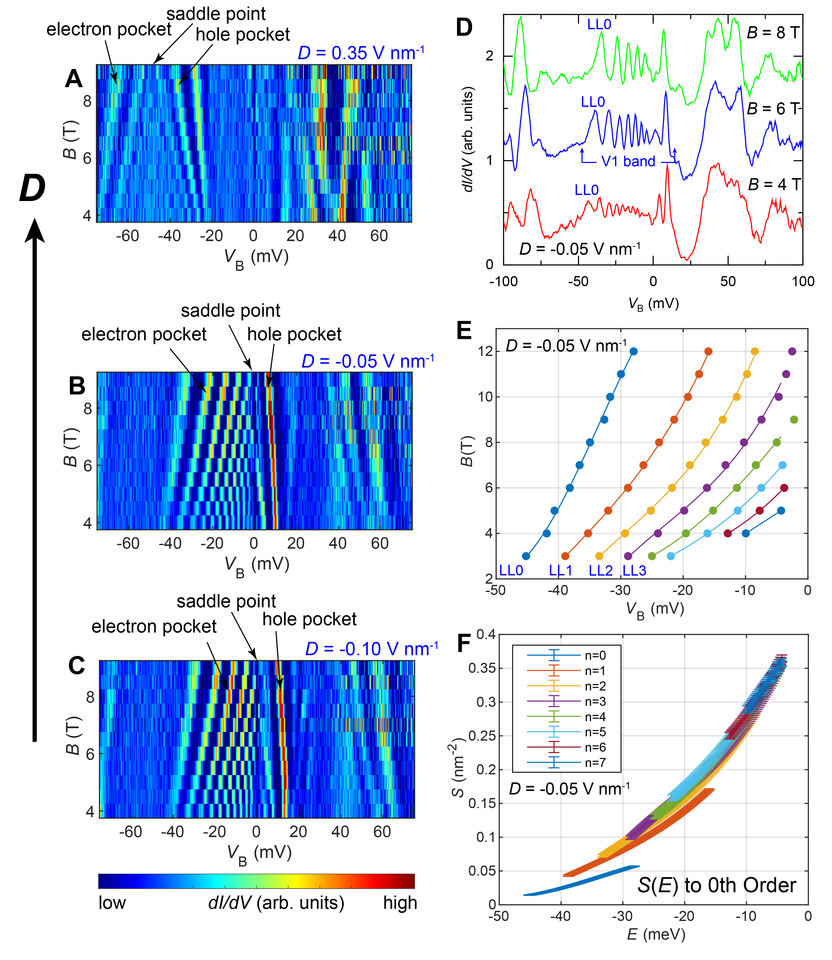
Application of a magnetic field creates sharp LLs in the dI/dV spectrum of all four bands, as shown in the dI/dV maps at 𝐵 = 4 T and 8 T in Fig. 2, B and D. All dI/dV maps with magnetic field are acquired on an ABBC site (see red dot in Fig. 1D). The experimental maps can be compared to the theoretical maps in Fig. 2, C and E, obtained from magnetic field-dependent quantum mechanical calculations, following the methods in. A series of LL spectra at different displacement fields are extracted from the experimental map at 𝐵 = 4 T (Fig. 2A). The LLs in the V1 band are clearly pronounced and show that the LL energies are irregularly spaced, exhibiting neither the equal spacing characteristic for a parabolic band nor the square root dependence on orbital index as observed in graphene.

Fig. 2. Tuning Landau levels in TDBG with displacement and magnetic fields. (A) Tunneling spectra vs. 𝑉_B of TDBG at selected displacement fields taken from the map in (B). Tunneling spectral maps in the 𝐷 vs. 𝑉_B plane at (B) 𝐵 = 4 T, and (D) 𝐵 = 8 T. The maps were acquired on the maxima positions in the moiré structure indicated by the red dot in Fig. 1D. Setpoints: 𝐼 = 200 pA, 𝑉_B = 150 mV for (B) and (D), T = 0.01 K. See fig. S11 to S13 for additional spectral map data. Corresponding theory maps for (C) 𝐵 = 4 T (quantum calculation) and (E) 𝐵 = 8 T (quantum calculation). Reference, https://www.science.org/doi/10.1126/science.adf2040.

Credit: NIST

A close examination of the LLs in Fig. 2 shows a breakdown of the Onsager relation. To see this, we zoom in on the LLs in the V1 band. Figure 3D shows extracted, well-resolved spectra at selected 𝐵-fields. In Fig. 3E we display the corresponding peak positions of the LLs in the V1 band vs. 𝐵 for 𝑛 = 0 … 8, showing how the Landau levels disperse with magnetic field. Landau levels are semiclassically described by Onsager’s quantization condition, which requires that the total phase accumulation over a cyclotron orbit be an integer multiple of 2𝜋. This yields 𝑆(𝐸𝑛)𝜙₀2𝜋 = 2𝜋𝐵_𝑛(𝑛 + 1/2), relating the 𝑘-space area 𝑆(𝐸_𝑛) of the zero-field iso-energy contour of the 𝑛^th Landau level 𝐸_𝑛 to the magnetic field 𝐵_𝑛, where 𝜙₀ = ℎ/𝑒 is the magnetic flux quantum, ℎ is Planck’s constant and 𝑒 is the elementary charge. With the equal energy 𝑘-space area scaling as 𝐵_𝑛(𝑛+1/2) for all LLs at energy 𝐸_𝑛, a plot of 𝑆 ∝{𝐵_𝑛(𝑛+1/2)}_{𝑛=0,1,2,…} versus LL energy for all LLs would collapse onto a single curve. From Fig. 3E, we plot 𝑆 ∝ {𝐵_𝑛(𝑛+1/2)}_𝑛=0…7 in Fig. 3F. The fact that experimental data points fail to collapse onto a single curve demonstrates the inadequacy of the Onsager relation and the need for higher-order corrections.

Fig. 3. Breakdown of the standard Onsager relation in TDBG. Spectral maps in the 𝐵 vs. 𝑉_B plane for displacement fields of (A) 𝐷 = 0.35 V nm^-1, (B) 𝐷 = −0.05 V nm^-1, and (C) 𝐷 = −0.1 V nm^-1 showing the dispersion of the electron and hole pocket LLs with magnetic field, and the shift of the V1 saddle point to lower energies with increasing displacement field. (D) Tunneling spectra vs. 𝑉_B of TDBG as a function of magnetic field at fixed 𝐷 = −0.05 V nm^-1. (E) LL peak positions vs. 𝐵 for 𝐷 = −0.05 V nm^-1. Data from LLs 𝑛 = 0 to 𝑛 = 8 are shown. Symbols: Experimental peak positions. Solid lines: Cubic-spline interpolation of experimental peak positions. (F) 𝑆(𝐸) computed from the solid lines in (E) using Eq. 1. The lack of data collapse indicates that second-order contributions to the LL energies are significant. Reference, https://www.science.org/doi/10.1126/science.adf2040.

Credit: NIST

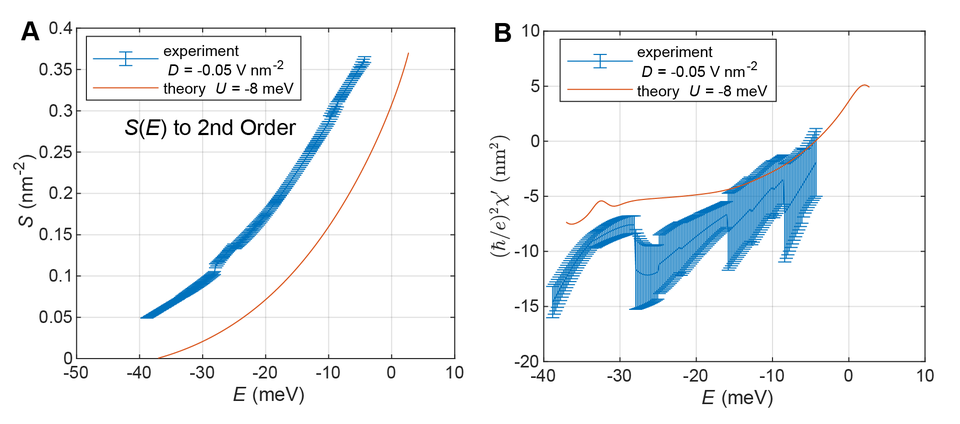
A further analysis of the LL energies allows the orbital area and derivative of the magnetic susceptibility to be obtained to second order as shown in Fig. 4.

Fig. 4. Extraction of enhanced energy-dependent orbital magnetic susceptibility in moiré quantum matter from the extended Onsager relation. (A) (symbols) 𝑆(𝐸) computed from the solid lines in Fig. 3E demonstrating data collapse onto one continuous curve. (solid line) 𝑆(𝐸) computed for the V1 band from semiclassical calculations. (B) (symbols) 𝜒′(𝐸) computed from the solid lines in Fig. 3E. (solid line) 𝜒′(𝐸) computed from semiclassical calculations. Reference, https://www.science.org/doi/10.1126/science.adf2040.

Credit: NIST