NIST TN 1297: 4. Type B Evaluation of Standard Uncertainty

4.1 A Type B evaluation of standard uncertainty is usually based on scientific judgment using all the relevant information available, which may include

Some examples of Type B evaluations are given in subsections 4.2 to 4.6.

4.2 Convert a quoted uncertainty that is a stated multiple of an estimated standard deviation to a standard uncertainty by dividing the quoted uncertainty by the multiplier.

4.3 Convert a quoted uncertainty that defines a "confidence interval" having a stated level of confidence (see subsection 5.5), such as 95 or 99 percent, to a standard uncertainty by treating the quoted uncertainty as if a normal distribution had been used to calculate it (unless otherwise indicated) and dividing it by the appropriate factor for such a distribution. These factors are 1.960 and 2.576 for the two levels of confidence given (see also the last line of Table B.1 of Appendix B).

4.4 Model the quantity in question by a normal distribution and estimate lower and upper limits a_- and a₊ such that the best estimated value of the quantity is (a₊ + a_-)/2 (i.e., the center of the limits) and there is 1 chance out of 2 (i.e., a 50 percent probability) that the value of the quantity lies in the interval a_- to a₊. Then u_j ≈ 1.48 a where a = (a₊ - a_-)/2 is the half-width of the interval.

4.5 Model the quantity in question by a normal distribution and estimate lower and upper limits a_- and a₊ such that the best estimated value of the quantity is (a₊ + a_-)/2 and there is about a 2 out of 3 chance (i.e., a 67 percent probability) that the value of the quantity lies in the interval a_- to a₊. Then u_j ≈ a, where a = (a₊ - a_-)/2.

4.6 Estimate lower and upper limits a_- and a₊ for the value of the quantity in question such that the probability that the value lies in the interval a_- to a₊ is, for all practical purposes, 100 percent. Provided that there is no contradictory information, treat the quantity as if it is equally probable for its value to lie anywhere within the interval a_- to a₊; that is, model it by a uniform or rectangular probability distribution. The best estimate of the value of the quantity is then (a₊ + a_-)/2 with u_j  = a/

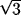
where a = (a₊ - a_-)/2.

If the distribution used to model the quantity is triangular rather than rectangular, then u_j  = a/

 .

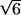
If the quantity in question is modeled by a normal distribution as in subsections 4.4 and 4.5, there are no finite limits that will contain 100 percent of its possible values. However, plus and minus 3 standard deviations about the mean of a normal distribution corresponds to 99.73 percent limits. Thus, if the limits a_- and a₊ of a normally distributed quantity with mean (a₊ + a_-)/2 are considered to contain "almost all" of the possible values of the quantity, that is, approximately 99.73 percent of them, then u_j  ≈ a/3, where a = (a₊ - a_-)/2.

The rectangular distribution is a reasonable default model in the absence of any other information. But if it is known that values of the quantity in question near the center of the limits are more likely than values close to the limits, a triangular or a normal distribution may be a better model.

4.7 Because the reliability of evaluations of components of uncertainty depends on the quality of the information available, it is recommended that all parameters upon which the measurand depends be varied to the fullest extent practicable so that the evaluations are based as much as possible on observed data. Whenever feasible, the use of empirical models of the measurement process founded on long-term quantitative data, and the use of check standards and control charts that can indicate if a measurement process is under statistical control, should be part of the effort to obtain reliable evaluations of components of uncertainty [8]. Type A evaluations of uncertainty based on limited data are not necessarily more reliable than soundly based Type B evaluations.