Modeling of Cement Paste Hydration and Microstructure Development
Summary:
Understanding the complex chemical changes that occur when cement powder is mixed with water is a long-standing but extremely challenging technological goal. These changes are termed hydration. Fundamental computational modeling of the hydration of cement is difficult because it involves a large number of coupled nonlinear rate equations that must be solved on a random three-dimensional spatial domain. To address these challenges, we are applying a new computational model called HydratiCA, which has several advantages over previous attempts to model cement paste hydration.
Visualization is important for validation of the model as development proceeds. It is also important to facilitate understanding the distribution of phases in 3D.
Description:
The HydratiCA model is based on concepts of transition state theory and uses stochastic cellular automaton algorithms to simultaneously model 3-D reaction and transport phenomena. This allows us to track the detailed kinetics and equilibria that occur in a diverse range of cementitious systems. At the length scales required to finely resolve the reaction mechanisms and microstructure changes in cement paste, HydratiCA must take small time steps (approximately 10-5 seconds) to remain numerically stable. In other words, tens of millions of time steps are required to simulate the behavior of cement paste for just one hour. Therefore, parallelization of the model is important so that we can model systems that are large enough to be realistic, avoiding finite size effects, and still be able to complete the simulations in a reasonable amount of time.
Additional Technical Details:
HydratiCA is based on concepts of transition state theory and uses stochastic cellular automaton algorithms to simultaneously model 3-D reaction and transport phenomena. This allows us to track the detailed kinetics and equilibria that occur in a diverse range of cementitious systems. At the length scales required to finely resolve the reaction mechanisms and microstructure changes in cement paste, HydratiCA must take small time steps (approximately 10-5 seconds) to remain numerically stable. In other words, tens of millions of time steps are required to simulate the behavior of cement paste for just one hour. Therefore, parallelization of the model is important so that we can model systems that are large enough to be realistic, avoiding finite size effects, and still be able to complete the simulations in a reasonable amount of time.
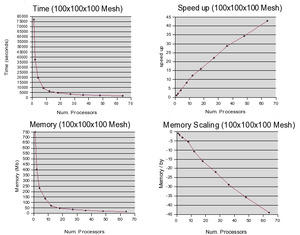
A standard spatial decomposition with regular subvolumes is used. Ghost nodes are used to keep the data current between processors. The code has been tested on the NIST's Linux cluster and found to scale well. Click on the following thumbnail image for graphs showing detailed performance results:
Major Accomplishments:
Publications
- J. Bullard, J. Hagedorn, T. Ley, Q. Hu, W. Griffin and J. Terrill. A Critical Comparison of 3D Experiments and Simulations of Tricalcium Silicate Hydration. Journal of the American Ceramic Society 101:4 (2018), 1453– 1470.
- Edward Garboczi , Jeffrey Bullard, Nicos Martys and Judith Terrill, The Virtual Cement and Concrete Testing Laboratory: Performance Prediction, Sustainability, and the CSHub in NRMCA Concrete Sustainability Conference , Tempe, AZ, April 13-July 15, 2010.
- Jeffrey Bullard, Edith Enjolras, William George , S. Satterfield and Judith Terrill, A parallel reaction-transport model applied to cement hydration and microstructure development, Modelling and Simulation in Materials Science and Engineering, 18, 2010. ID: 025007.
Note: Modelling Simul. Mater. Sci. Eng. 18 (2010) 025007 (16pp)doi:10.1088/0965-0393/18/2/025007
Return to High Performance Computing

