ACMD Seminar: The intimate connection between the fractional integrals and the time-fractional Porous Medium Equation (fPME)

Udita Katugampola, Ph.D.
Assistant Professor of Mathematics, Florida Polytechnic University

Thursday, April 19, 2018 15:00 - 16:00
Building 101, Lecture Room C
Gaithersburg

Thursday, April 19, 2018 13:00 - 14:00
Room 1-4072
Boulder

Host: Ryan Evans

Abstract: It is argued that the fractional operators naturally appear in certain modeling approaches, especially when the governing equations have terms that mimic certain "frictional-type of effects." So, two questions we struggle to answer are that "when and why fractional operators appear in model equations?" In the quest of finding answers to these questions, in this talk we study some properties of a generalized fractional integral which unifies six familiar fractional integrals into a unique form given by

We obtain a series representation of this integral along with asymptotic expansion and use it to solve a time-fractional porous medium equation in a subdiffusive case (0 < α < 1) of the form

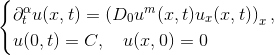
where 

 is the Riemann-Liouville fractional derivative of order α. We show that Erdélyi-Kober type integral naturally appears in the model equation which then be replaced by the integral in question. We study several cases of m to illustrate the applicability of this approach. Also, we drive two new identities of Taylor-type which can be used in broader sense. We also study some asymptotic approaches for numerical solutions which are in excellent agreement with the exact solution.

Bio: Udita N. Katugampola is an assistant professor of mathematics at Florida Polytechnic University (FL Poly). His primary research areas are in fractional calculus and combinatorics with the intension of finding “real world” applications of fractional operators. One of his major achievements is the unification of Riemann-Liouville and Hadamard fractional operators into a unique form, which is now known in the literature as “Katugampola fractional integral” that has many applications in applied mathematics and other areas. He also received a U.S. Army research grant in the amount of $300k for his work on fractional calculus. After graduating from Southern Illinois University at Carbondale, he joined Delaware State University as a visiting assistant professor before joining University of Delaware and now he is with FL Poly as a faculty member.