Theory of the optical properties of materials

Summary

The overarching objective of this project is reliably calculating the bulk optical properties of materials, such as complex index of refraction, absorption, and reflectance, across the electromagnetic spectrum. In doing so, we gain insight into the atomic geometry, structural properties and electronic structure of materials, and improve our ability to predict properties of heterogeneous systems such as photonic crystals and optical fibers.

Description

Around 1998, first-principles calculation of optical constants and dielectric response began to include excitonic effects. Beginning with simple, wide-gap insulators and semiconductors, the field has progressed to studying more complex materials, clusters, and so forth. In the area of core excitations, one can even include multiplet effects in certain circumstances. And, it is now becoming routine to include lifetime-damping effects that broaden features in excitation spectra due to the finite lifetimes of excited states.

The vast majority of this work is based on solving the Bethe-Salpeter Equation (BSE) at a practical level of approximation. NIST maintains two BSE calculation methods, one for valence excitations (near-infrared to near-ultraviolet) and one for core excitations (x-ray). We also maintain an atomic structure calculation program that interfaces with the NIST BSE code for core excitations, allowing us to study many atomic effects on demand in the context of core excitations.

We are currently limited in the scope of systems that can be easily studied with BSE calculations by the extensive effort required to calculate dielectric screening effects and electron and hole lifetime-damping effects. Thus, we are seeking to identify the salient aspects of dielectric response and formulate model dielectric functions and one-electron self-energies to advance the frontier of BSE calculations. We are also investigating alternatives for the implicit "one electron plus one hole" or "one-plus-one" paradigm in practical BSE calculations.

Examples:

 

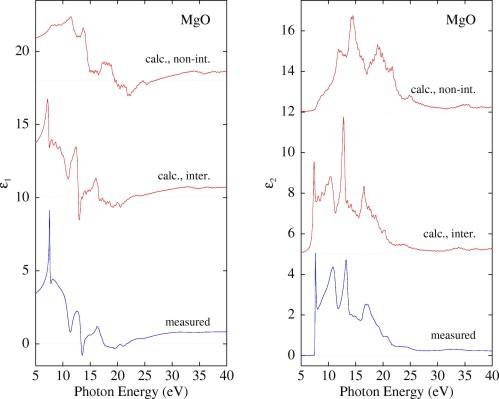
This figure illustrates a frequent success of BSE work: the appearance of observed features in calculated spectra only if excitonic effects are included in the calculation. Here, the real and imaginary parts of the dielectric function of magnesium oxide (MgO) are shown.

 

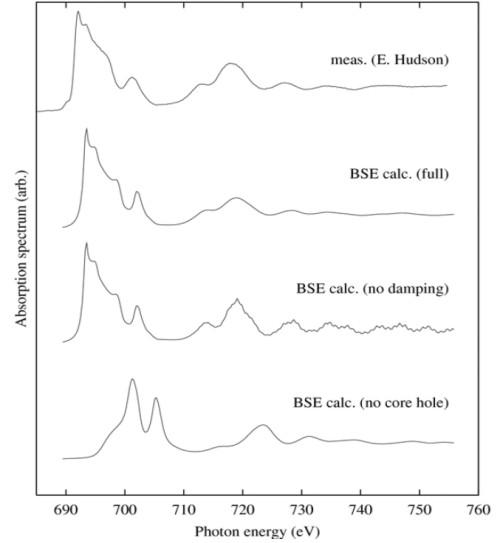
Similar to the previous figure, this figure also demonstrates the success of calculations incorporating excitonic effects. The spectra shown above represent the fluorine (F) core edge in lithium fluoride (LiF). The top spectrum was obtained experimentally, the second spectrum was calculated including excitonic and lifetime-damping effects, and the third and fourth spectra were calculated omitting either lifetime-damping or excitonic effects, respectively.

 

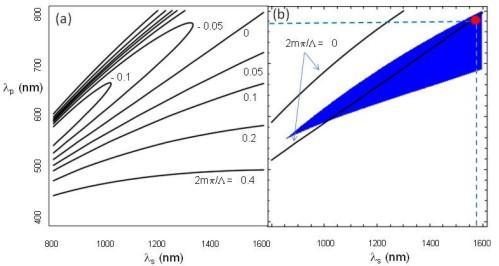
We have recently begun to provide theoretical guidance for quantum information in solid-state systems. In support of the development of a heralded single-photon source, we calculated that a 3 μm wide strip of rubidium diffused in a potassium titanyl phosphate substrate (RTP/KTP) can achieve type-II phase-matched operation in the 1550 nm telecommunications band without the need to pole the crystal to achieve quasi-phase matching. (a) The phase mismatch of a signal and idler photon for various wavelengths are shown. (b) The blue region represents those wavelength combinations which support a heralded single-photon source with both the signal and idler wavelengths no more than 1600 nm; the solid lines represent the combinations for which phase matching is achieved without poling; and the red dot represents a preferred operating point.

Major Accomplishments

• The NBSE project is one of the earliest, most comprehensive projects worldwide that incorporates excitonic effects in optical spectra with such success, representing a paradigm shift in calculations of the optical properties of materials.
• In collaboration with NIST Physicist John Burnett, we discovered a spatial-dispersion-induced birefringence in calcium and barium fluoride that was sufficiently large to impact semiconductor manufacturing. Inclusion of this effect allowed the industry to progress from 248 nm lithography to 193 nm lithography, which is still (as of 2009) in use.

Associated Product(s)

The valence NBSE program has been equipped with a user-friendly interface so that all inputs are written in a clear and portable data format. Furthermore, the John Rehr Group at the University of Washington of Seattle has prepared a utility that translates output of a popular density-functional band-structure program into input suitable for the valence NBSE.  

The interface is maintained at the University of Washington.

For more information, see Optical to UV spectra and birefringence of [quartz, rutile and anatase]: First-principles calculations with excitonic effects.