Quantum anomalous Hall effect Theory

Summary

Quantum anomalous Hall materials exhibit a well-quantized Hall resistance at low temperatures. To increase the operating temperature for these materials, it’s necessary to understand and mitigate the material disorder and to identify materials with a large topological band gap. We utilize theoretical tools to understand (quantitatively and microscopically) the impact of disorder on the quantization of the Hall response, with the aim of developing strategies to mitigate its impact. We also develop theoretical tools for understanding the optical response of these materials, which can offer a route to characterizing the disorder and its impact on electronic transport.

Description

The quantum anomalous Hall effect is a phenomenon in which certain magnetic insulators exhibit a zero-field Hall resistance value, 𝑅_𝐻, that is precisely quantized in terms of fundamental constants of nature:
𝑅_𝐻 = ℎ/𝑛𝑒², where ℎ is Planck's constant, 𝑒 is the charge of the electron and 𝑛 is a material-dependent integer. This effect is a cousin of the quantum Hall effect, which exhibits the same behavior but requires a rather large external magnetic field. Both effects occur in materials with small but non-negligible disorder. The presence of a nearly perfectly quantized Hall resistance in materials with a multitude of random impurities is extraordinary. The robust behavior of this system is due to the topology of the material’s electronic structure.

The mathematical term for the key topological property is the Chern number. This is a so-called “topological invariant” that characterizes important electronic properties of insulators. The Chern number is the integer n that enters into the quantized Hall resistance. The robustness of the Chern number to mild distortions of the electronic structure - from things like disorder - underpins the robustness of the observed Hall resistance. The observation of the quantum Hall effect and its subsequent explanation in terms of topology have led to multiple Nobel prizes, and to our current definition of the ohm.

Our group is interested in the impact of disorder on the quantum anomalous Hall effect. Disorder is quite strong in the most well-studied quantum anomalous Hall material, magnetically doped topological insulators. This is likely the reason for a well-quantized response which occurs only at very low temperatures. To understand the role of disorder in these and related systems, we utilize techniques ranging from the Kubo formula to non-equilibrium Green’s functions.

Below are results that show the numerically computed current that flows in a topological insulator with random magnetic dopants. This was obtained using non-equilibrium Green’s function, which describes electronic transport in the Landauer-Buttiker picture of mesoscopic physics.

Real-space visualization of the current and non-equilibrium charge distribution in a quantum Hall system

Credit: NIST

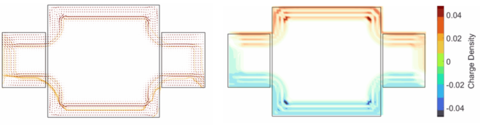
Another focus of the group is the development of linear and nonlinear optical response as a probe of both the material’s topological properties and disorder. It has been recently recognized that the optical response can be framed in terms of the electronic structure topology, through the quantum geometry, which encompasses the quantum metric and the Berry curvature. The spatial dependence of the linear and nonlinear response should hold a wealth of information about the material’s electronic structure geometry and its spatial variation. We are developing and applying the theoretical description of the optical response and have applied our work to other systems, such as metallic thin films. Our aim is to apply this to various quantum anomalous Hall effect materials and propose a way of probing the effects of disorder on the Hall response, both with high resolution with near-field optical techniques and with high throughput using standard optical scanning techniques.

Our group has expertise in other "flavors" of Hall effects, such as the spin Hall effect.  The conventional Hall effect, described in the previous paragraphs, describes the perpendicular flow of electron charge in response to a driving electric field. The spin Hall effect describes the perpendicular flow of electron spin in response to an applied electric field.  Both conventional Hall and spin Hall effects share similar origins. However, there are important differences between the two effects which can be traced back to the difference in conservation for charge and spin: charge is conserved while spin is not. We’ve computed the intrinsic spin Hall effect in ferromagnetic materials, which has important implications in spintronics. We have also studied the related orbital Hall effect and showed that its experimental signatures can occur as a real space modulation of the charge density distribution, or as a change in the material optical response.