Diffraction effects in radiometry

Summary

We want to quantify the breakdown of geometrical optics when computing the throughput of optical systems for the purpose of calculating "diffraction corrections" to radiometric measurements. We maintain an evolving suite of computer programs that we use to compute diffraction corrections for ourselves and external customers and better understand the phenomenon of diffraction as it impacts radiometry. We are also packaging the programs so that we can help others compute diffraction corrections on their own. The computational work is built on the foundation of mathematical derivations of diffraction effects and our ensuing simplifications of the results of those derivations.

Description

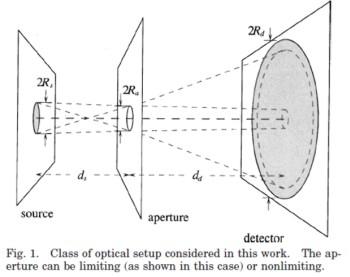
Essentially, classical radiometry relies on geometrical optics (to relate source radiance), geometrical aspects of an optical layout, and the irradiance at the detector.  One considers the propagation of radiation from points on the surface of the source to points on the surface of the detector.  In reality, the wave nature of light causes light to diffract at the edges of intervening apertures, mirrors, and lenses. Diffraction can also result in diffraction-limited focusing.  Overall, these effects can give rise to losses or gains of flux reaching the detector.

To infer one quantity from an optical radiometric measurement, such as source radiance, detector response, aperture area, and so forth, one must know all other pertinent quantities in the measurement.  Yet the measurement equation that relates various quantities should also consider the effects of diffraction.  Diffraction causes the actual throughput of an optical system to differ from its geometrical throughput.  One must calculate the diffraction effects in order to incorporate the above difference in throughput in final results.  This step is typically referred to as including "diffraction corrections." 

We have developed a robust suite of computer programs that allow one to specify an optical setup and determine diffractions effects on throughput as a function of wavelength, or, in the case of a Planck source, of temperature.  We have studied several multi-stage systems, and have conducted the most thorough investigations in those systems that can be "unfolded" to yield a (nearly) symmetric system and/or can be treated in terms of subsystems, each of which consists of a source, a single aperture or lens, and a detector  (such subsystems are denoted by the acronym, SAD).

Major Accomplishments

• This project has provided theoretical support since 1995 to the Low-Background Infrared (LBIR) Facility. This led to the computational methods that were part of the effort cited in the 2005 US DOC Bronze Medal Award, presented to E.L. Shirley and A.C. Carter, "For developing innovative computational and experimental methods to accurately calibrate infrared sensors used in missile defense," as well as cited in the 2020 US DOC Bronze Medal Award, presented to T.A. Germer and E.L. Shirley, “For advancing the theory and measurement of light-scattering and diffraction effects that often limit the accuracy of optical radiation measurements.”
• We have found diffraction effects to be significant (on the tenth-of-a-percent level) in the case of current space-borne total-solar-irradiance monitors. Hence, our diffraction corrections are an important aspect of the overall effort to understand the role of solar variation in climate, as decadal changes in its radiance on the level of 0.02 percent (200 ppm) are significant. This was part of the effort cited in the 2012 US DOC Gold Medal Award, “For providing the measurement science and models, at the level of accuracy and in the time-frame required, to unambiguously assess the effect of the Sun on climate change.”
• We have discovered compact representations for asymptotic expansions of diffraction effects at short wavelengths (relevant to spectral power measurements) and high temperatures (relevant to total power measurements).  These formulas are useful because their validity is pertinent in exactly the wavelength or temperature regions where numerical calculations can become too costly.
• We have developed a formulation for calculating higher-order diffraction effects that will permit us to account for effects of light being diffracted in series at two or more edges.  Usually, diffraction formulas exist only for diffraction by single edges.  This higher-order formulation will help extend the range of validity of the above asymptotic expansions.

Associated Product(s)

Several of our computer programs are being refined and packaged to be usable by others.  Announcements pertaining to this will be made in due course.