
We're Hiring!
Please visit the CAISI Careers Page to learn more about our open roles and opportunities.
Improving the validity and robustness of AI system evaluations is an ongoing goal of NIST AI measurement science efforts. A new publication from NIST’s Center for AI Standards and Innovation (CAISI) and Information Technology Laboratory (ITL) aims to help advance the statistical validity of AI benchmark evaluations: NIST AI 800-3 Expanding the AI Evaluation Toolbox with Statistical Models.
Key Contributions
Benchmark-style evaluations are one important tool for understanding the performance of AI systems. However, common approaches to analysis and reporting of benchmark results may (1) rely on implicit assumptions, (2) conflate different notions of system performance, or (3) fail to accurately quantify uncertainty. When present, these gaps make it difficult or impossible to interpret and make decisions based on benchmark evaluation results.
In NIST AI 800-3, we develop a statistical model for AI evaluations which formalizes evaluation assumptions and measurement targets. Contributions include the following:
- We distinguish two measures of performance — benchmark accuracy (performance on the set of questions included in a benchmark) and generalized accuracy (performance across the broader universe of questions similar to those in the benchmark). Benchmark and generalized accuracy may meaningfully differ and therefore must be calculated in different ways, as depicted in the figure below.
- In addition to reviewing and expanding existing methods to estimate these accuracy metrics, we demonstrate an approach based on generalized linear mixed models (GLMMs). GLMMs are an established technique in other fields yet not commonly employed among AI evaluators.
- GLMMs enable evaluators to estimate latent AI system capabilities and gain useful insights into benchmark composition and LLM performance. In many cases, GLMMs more precisely quantify the uncertainty of LLM performance measurements compared to current techniques. We illustrate the advantages of the GLMM approach using data from the evaluation of 22 frontier Large Language Models (LLMs) on three common LLM benchmarks: GPQA-Diamond, BIG-Bench Hard, and Global-MMLU Lite.
These results are relevant to evaluators, practitioners, procurers, and developers of AI systems who are looking to better understand and communicate AI performance from a rigorous and principled statistical perspective. Our statistical framework and techniques demonstrate an expansion of the current toolbox of evaluation practices, providing a pathway towards increased robustness in AI measurement and deeper understanding of widely-relied-upon benchmarks.
In the following sections, we provide a brief overview of NIST AI 800-3’s key contributions.
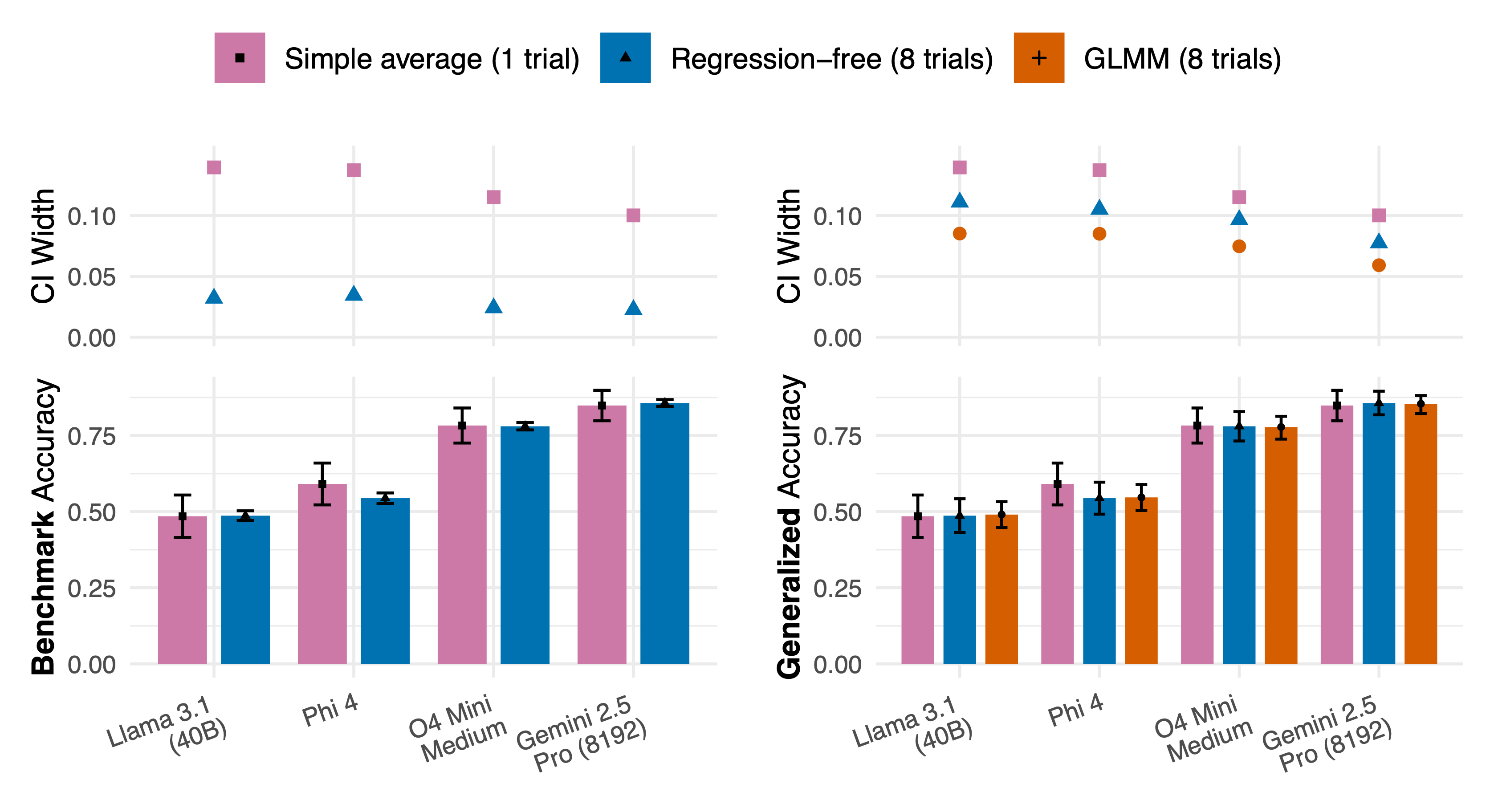
Comparing accuracy estimates (GPQA-Diamond). Lower plots show the estimated accuracy of a selection of tested LLMs* with 95% confidence intervals. Upper plots show corresponding confidence interval (CI) widths. Generalized accuracy CIs are larger than benchmark accuracy CIs because they account for the selection of benchmark items from a superpopulation. Notably, some pairs of LLMs may have significantly different benchmark accuracy but not generalized accuracy. The simple average (pink) estimates reflect the average across all n benchmark questions with standard error calculated as standard deviation of results divided by √n. For estimates of benchmark accuracy, the simple average method results in under-confident CIs compared to a valid regression-free method (blue). For estimates of generalized accuracy, the simple average method provides valid CIs, but precision can be increased by running more trials per item (as in the regression-free method). Generalized linear mixed model (GLMM, orange) estimates require additional assumptions but further increase precision.
Explicitly Defined Performance Metrics
Evaluators often report a single accuracy metric: the proportion of correct outputs across a benchmark's items. This single metric can be seen as aiming to answer one of two distinct questions: First, how well does the LLM perform on this specific, fixed benchmark? Or, more broadly, how well would the LLM perform across the larger population of questions similar to those in the benchmark? As mentioned above, NIST AI 800-3 formally defines two distinct measures of performance corresponding to each of these questions: benchmark accuracy and generalized accuracy.
There is no one-size-fits-all formula for quantifying AI performance in an evaluation. Rather, it is the evaluator's role to determine the best method to compute performance statistics and describe uncertainty based on evaluation goals and benchmark data. Often, evaluators seek to treat benchmark questions as representative of a larger set in order to make broader statements about an LLM’s performance – making generalized accuracy a reasonable metric. Regardless of an evaluator’s choice, explicitly defining the measure of accuracy used allows for clearer articulation of results and their uncertainty.
Statistical Methods to Estimate Accuracy
We show that these accuracy estimands require different estimation methods in order to properly quantify uncertainty. Evaluators often estimate accuracy via “regression-free” methods – in particular, computing accuracy as the grand mean of question scores – though they may fail to clarify which notion of accuracy (generalized or benchmark) they are targeting. NIST AI 800-3 compares these regression-free approaches to an alternative using generalized linear mixed models, akaGLMMs.
Using both real and simulated benchmark data, we show that when well specified, GLMMs produce similar generalized accuracy point estimates to a regression-free approach while more efficiently estimating uncertainty, as illustrated in the figure above. GLMMs rely on more assumptions about benchmark data than regression-free methods, but also provide some means of checking these assumptions – which can help surface issues with benchmark design.
GLMMs-Enabled Explanatory Statistics
Statistical modeling can equip evaluators with important context on evaluation results. GLMMs produce explanatory statistics that can improve evaluators' understanding of benchmark composition and LLM performance, including estimation of latent LLM capability measures and benchmark question difficulties. For example, question difficulty estimates (illustrated below for GPQA-Diamond) can help identify potentially problematic questions and reveal benchmark-level patterns.
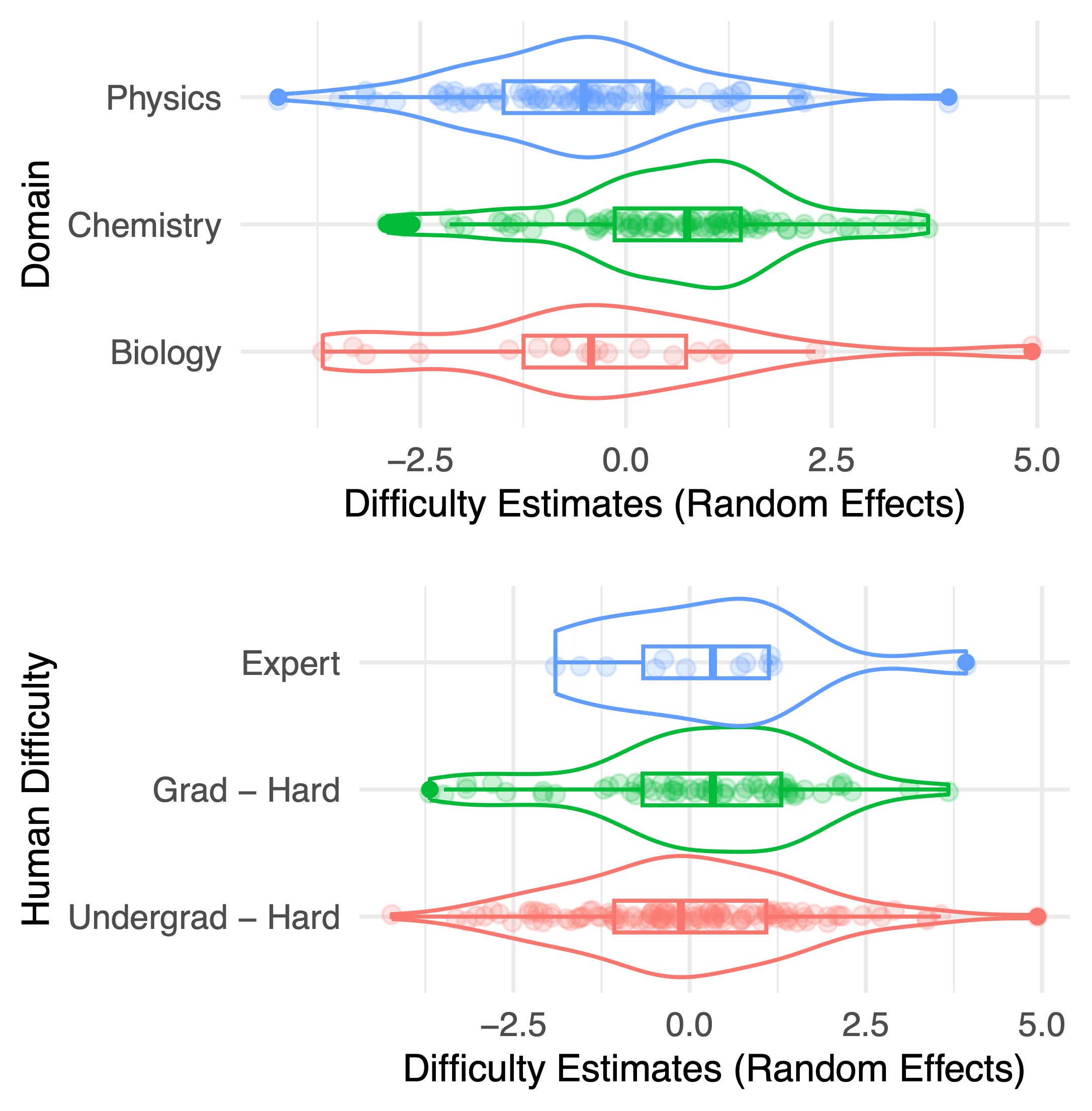
Distribution of estimated question difficulties by domain and labeled difficulty (GPQA-Diamond). Each dot indicates a GPQA-Diamond question’s GLMM-estimated difficulty (i.e., random effect value). Box plots display quartiles and violin plots display estimated density. These estimates show that GPQA-Diamond’s chemistry questions were particularly difficult for the 22 tested LLMs. On the other hand, question difficulty for LLMs has a weak relationship with question-writer-labeled difficulty. This may suggest that humans and the tested LLMs find different questions difficult, and/or could call into question whether writer annotations are accurate even for human difficulty.
GLMMs enable decomposition of the total variance in evaluation results into a between-question component reflecting differences in LLM performance between different questions, and a within-question component reflecting inconsistency in LLM performance on the same question. We use BIG-Bench Hard and Global-MMLU Lite as examples of the utility of such decomposition, illuminating differences between tasks and languages. For instance, a set of tested LLMs scored roughly 83% on average on two BIG-Bench Hard tasks: “Penguins in a Table”, which consists of word problems involving simple tables of data, and “Formal Fallacies”, which asks LLMs to decide whether logical statements are valid or invalid. However, GLMM-derived statistics reveal that the LLM results are more consistent for each individual Table question than for each Formal Fallacies question, while conversely there is more variation in performance between Table questions than between Formal Fallacies questions.
Looking Ahead
NIST AI 800-3 argues that the statistical validity of LLM evaluations benefits from evaluators explicitly adopting a model for analyzing evaluation results and disclosing related assumptions. Generalized linear mixed modeling is one promising approach which could form a foundation for more principled AI evaluation statistics. Future CAISI and NIST publications will further explore the application of statistical models to AI evaluation. We look forward to engaging with industry and the scientific community as research on this topic continues to develop. Questions and comments can be directed to caisi-metrology [at] nist.gov (caisi-metrology[at]nist[dot]gov).
* The identification of commercial AI systems in this figure and paper does not imply recommendation or endorsement of any product or service by NIST, nor does it imply that the systems identified are necessarily the best available for a purpose.

