Taking Measure
Just a Standard Blog

Happy Pi Day! No, not pie day, Pi Day. That Greek character pi, π, that you’ve heard of but aren’t quite sure what the big deal is. Pi is the ratio of a circle’s circumference to its diameter. As yawn-inducing as that may sound, it’s an important ratio because pi is the same no matter the size of the circle.
This magical ratio, pi, is true for the circle describing the tire of an automobile or a circle going around the entire Earth. We can use pi to calculate a diameter. If the circumference of the Earth at the equator is 40,075 kilometers, which it is, then the diameter of the Earth is equal to the circumference divided by pi, which is approximately 12,756 kilometers.
Pi is also an “irrational” number. That doesn’t mean it’s crazy or unreasonable, but it does mean that there is a never-ending set of digits in the number pi, i.e. 3.141592653589…. Since pi has this screwy irrational property, it cannot be written down exactly no matter how much paper you have. Back in 1706, someone had the bright idea of using a symbol, π, to stand for the ratio without worrying about all that digit stuff. There is a terrific Scientific American article, “What is pi and how did it originate” that details some of the number’s fascinating origins.
We celebrate Pi Day on March 14 because it’s 3/14!
Because pi is used in many equations, it appears a fair number of times in an important mathematical reference offered by NIST: the Digital Library of Mathematical Functions or DLMF (available online and on paper).
A mathematical function is a well-defined relation between two or more varying quantities. In the simplest case, a function shows how one quantity (the dependent variable) changes as a second (the independent variable) increases or decreases. Many such functions, like sine, tangent, logarithm and exponential are studied in trigonometry. But there is a whole zoo of such functions that pop up when scientists try to understand the workings of the physical world. The DLMF provides all the information scientists need to work with mathematical functions.
One of the coolest aspects of the online version of the DLMF is the ability to interact with a graphical representation of the mathematical function right there in your Web browser!
This version of the DLMF is actually a sequel to the classic 1964 “Handbook of Mathematical Functions,” aka Abramowitz and Stegun for its two editors Milton Abramowitz and Irene Stegun. Over the years, the Handbook has become the most widely cited publication in NIST’s history.
In fact, the esteemed editors of Wikipedia say, “The notation used in the Handbook is the de facto standard for much of applied mathematics today.”
At over 50 years old, however, it seemed like a good idea for us to update and improve the accessibility and functionality of the document. Today, we can provide much more functionality, such as searching for equations. We can even search for equations containing π! These modern publishing capabilities take advantage of the Internet to make the DLMF even more useful to the research community and public at large.
So, now that we have this book and website with oodles of equations, what do we do with it? In many cases the equations are used as part of some measurement task. Here at NIST measurement is taken very seriously; it’s what we do! More important than NIST doing measurements, however, is helping others to make better measurements. The DLMF is an authoritative resource thousands of researchers use to do just that.
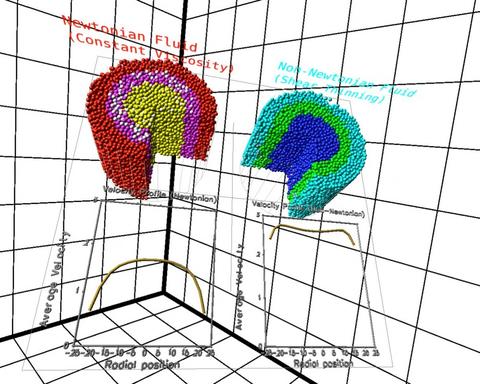
As an example, let’s talk about something really exciting like watching concrete dry! Well, “cure” really. While it has been used in construction for thousands of years, exactly how concrete works is still somewhat of a mystery. One of NIST’s measurement goals, understanding the complex chemical changes that occur when cement powder is mixed with water, is a long-standing, but extremely challenging, technological goal. Why study concrete? You know all those buildings and bridges that are made with concrete, well, if the concrete cures incorrectly and can’t support the weight it’s supposed to support, bad things can happen.
One way to figure out what’s going on inside the concrete is to do computer simulations. This means creating a virtual model using all sorts of very complicated mathematical equations. The mathematical model of the concrete’s lubrication force, which tells us how fast different areas of the flowing concrete are moving, includes calculations that use (you guessed it!) pi.
So, as you can see, pi shows up everywhere there are circles and spheres, even in the concrete beneath your feet.
Now go get some pie!
*Edited July 31, 2019, to repair a broken link





