Cybersecurity Insights
a NIST blog

In this series, we've examined several different ways to answer queries over data using differential privacy. So far each approach requires changing the way we answer queries - usually by adding noise to the answer - and modifying the tools we would normally use for analyzing data.
What if we want to use existing data analysis tools, but still protect privacy? For example, the marketing department of our pumpkin spice latte company might be accustomed to exporting sales data to a spreadsheet at the end of each month to analyze sales trends using a popular spreadsheet application. They would like to better protect individuals’ privacy, but don’t want to learn--or buy--new tools.
One approach is to produce a “de-identified” or “anonymized” version of the data for use by the marketing department. This data looks like the original dataset, but identifying information is redacted. This anonymized data can then be analyzed using any tool the marketing department likes. Unfortunately, as described in our first post, this approach does not prevent re-identification of individuals.
Can we achieve the same workflow, except use differential privacy to better protect privacy? The answer is “yes”: using techniques for generating differentially private synthetic data. A differentially private synthetic dataset looks like the original dataset - it has the same schema and attempts to maintain properties of the original dataset (e.g., correlations between attributes) - but it provides a provable privacy guarantee for individuals in the original dataset.
It's important to note that many techniques for generating synthetic data do not satisfy differential privacy (or any privacy property). These techniques may offer some partial privacy protection, but they do not give the same protection backed by mathematical proof as differentially private synthetic data does.
Use Cases & Utility
Differentially private synthetic data has a huge advantage over other approaches for private data analysis: as shown in Figure 1, it allows analysts to use any tool or workflow to process the data. Once the data has been “privatized,” no further protection is required. The differentially private synthetic data may be analyzed, shared, and combined with other datasets, with no additional risk to privacy. This property makes differentially private synthetic data much easier to use than the approaches we have discussed previously--all of which require modifying the tools and workflows used to analyze data.
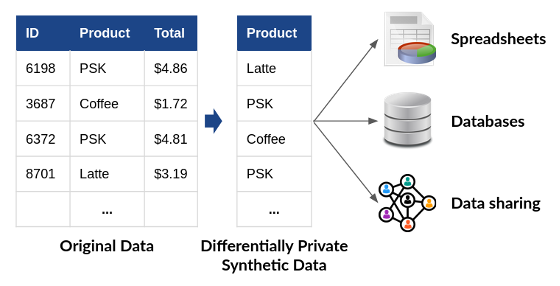
The primary challenge of differentially private synthetic data is accuracy. Constructing accurate differentially private synthetic data turns out to be extremely challenging in practice. As a rule of thumb, a purpose-built differentially private analysis, like the ones described in previous posts, will generally yield better accuracy than the same analysis on synthetic data. However, tools for this purpose are developing rapidly. In 2018, NIST conducted a Differential Privacy Synthetic Data Challenge, which attracted submissions based on many different techniques. For the benchmark problems considered in the Challenge, the top-scoring solutions produced extremely accurate differentially private synthetic data. More on these solutions later in the post.
On the other hand, a high degree of accuracy is not essential for every use case. Sometimes rough accuracy is enough to provide you with the insights and trends that you need to meet your objectives. Differentially private synthetic data can be an excellent solution in these scenarios.
Generating Synthetic Data
Conceptually, all techniques for generating synthetic data--privacy-preserving or not--start by building a probabilistic model of the underlying population from which the original data was sampled. Then, this model is used to generate new data. If the model is an accurate representation of the population, then the newly generated data will retain all the properties of that population, but each generated data point will represent a "fake" individual who doesn't actually exist.
Building the model is the most challenging part of this process. Many techniques have been developed for this purpose, from simple approaches based on counting to complex ones based on deep learning. The submissions to NIST’s Differential Privacy Synthetic Data Challenge spanned the spectrum of these techniques; the top 5 scoring algorithms in this challenge were released as open-source software, and are available on the NIST Privacy Engineering Collaboration Space. The rest of this post will describe the ideas behind two of these approaches.
Software Tools: Marginal Distributions
Imagine that we'd like to generate synthetic sales data for our pumpkin spice latte company. One way to accomplish this is using a differentially private marginal distribution, as in Figure 2. From the original tabular data, we construct a histogram by counting the number of each drink sold. Next, we add noise to the histogram to satisfy differential privacy. Finally, we divide each noisy count by the total to determine what percentage of all drinks were of the specific type. This final step produces a one-way marginal distribution - it considers only one attribute of the original data and ignores correlations between attributes.
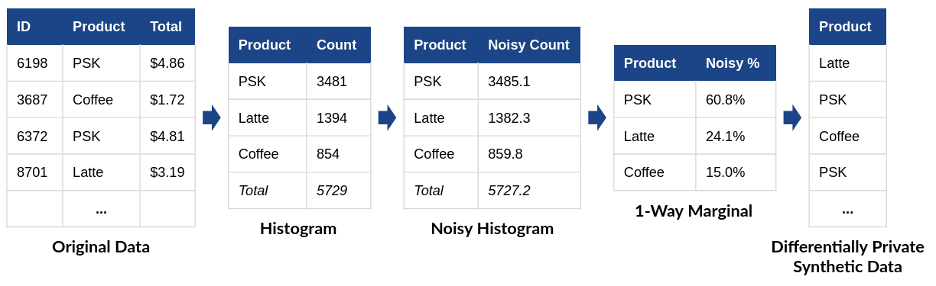
(PSK = Pumpkin Spice Latte)
Now, we can use the one-way marginal to generate a “fake purchase” using weighted randomness. We pick a drink type at random - but with the randomness weighted according to the one-way marginal we have generated. In the example in Figure 1, 60.8% of the generated purchases should be pumpkin spice lattes, 24.1% should be lattes, and 15.0% should be regular coffees.
Marginal distributions form the basis for many differentially private synthetic data algorithms, including the top-scoring algorithm from the 2018 NIST Challenge. The major challenge of this approach comes in preserving correlations between data attributes. For example, our sales data might include the customer's age in addition to the drink type - and age might be highly correlated with drink type (younger customers, we might imagine, are more likely to purchase pumpkin spice lattes than other drink types). We can repeat the process used above on both data attributes separately - but that approach doesn’t capture the correlation that was present between the two.
We can preserve this correlation by calculating a two-way marginal - a distribution over both data attributes simultaneously. But this marginal has many more possible options (all of the possible combinations of age and drink type), and it will result in a weaker "signal" relative to the noise for each option.
Preserving correlations like these requires a careful balance between the marginals being measured and the strength of the signal being preserved. The winning algorithm in the 2018 Challenge, submitted by Ryan McKenna, uses a differentially private algorithm to detect correlations in the data, and then measures 3-way marginals that include correlated attributes. This approach ensures that correlations are preserved, while maintaining a high signal strength. The second, third, and fourth place finishes in the Challenge also used an approach based on marginal distributions.
Software Tools: Deep Learning
Another way to build a model of the underlying population from the original data is with machine learning techniques. In the past several years, deep learning-based methods for generating synthetic data have become extremely capable in some domains. For example, thispersondoesnotexist.com uses a Generative Adversarial Network (GAN) - a type of neural network for deep learning - to generate convincing photos of imaginary people. The same approach can be used to generate synthetic data in other domains - like our latte sales data, for example - by training the neural network on original data from the right domain.
To protect the privacy of individuals in the original data, we can train the neural network using a differentially private algorithm. As we will discuss in a later post, several algorithms have been proposed for this purpose, and open-source implementations for popular deep learning frameworks have implemented these algorithms (e.g., TensorFlow Privacy and Opacus). If the neural network modeling the underlying population is trained with differential privacy, then by the post-processing property, the synthetic data it generates also satisfies differential privacy.
A GAN-based approach was used in the fifth-place submission to the 2018 NIST Challenge, submitted by a team from the University of California, Los Angeles. In general, deep learning-based approaches for differentially private synthetic data are less accurate than the marginal-based approaches discussed in the last section for low-dimensional tabular data (like the data in our latte example). However, this is an active area of research, and approaches based on deep learning may prove extremely effective for high-dimensional data (e.g., images, audio, video).
Coming Up Next
So far, this series has focused on how differential privacy works and how to apply differential privacy to answer interesting questions about data. However, implementation of differential privacy alone is not enough to protect privacy – it has to be implemented correctly. This correctness can be hard to achieve because differential privacy is implemented in software, and all software is prone to implementation bugs. This is a particular challenge because buggy differentially private programs don't crash – instead, they silently violate privacy in ways that can be hard to detect. Our next post will discuss tools and techniques which can ensure that differential privacy is implemented correctly in a particular application, as well as the limitations of traditional approaches to software assurance in the context of differential privacy.
This post is part of a series on differential privacy. Learn more and browse all the posts published to date on the differential privacy blog series page in NIST’s Privacy Engineering Collaboration Space.



