Magnetic Nanostructures for post-CMOS Electronics

Summary

Our goal is to address the metrology of magnetic effects at the nanoscale level. Nanomagnet arrays form the basis for major data storage technologies, notably magnetoresistive random access memory and bit-patterned media for ultra-high density storage devices. Moreover, the semiconductor industry is looking beyond conventional CMOS processing, where current lithography techniques are expected to fail.Although fabrication methods for post-CMOS circuitry have not been established, it is certain that the magnetic components involved will be in the nanometer range.Although defects are expected to dominate device behavior at this range, the metrology of defect-induced magnetic effects has not been developed at this scale.

Description

We focus primarily on arrays of magnetic nanostructures in order to reveal how defects alter the fundamental physics of magnetization reversal processes in the nanometer regime. We have an integrated approach that consists of four inter-related elements. The first element, film edge metrology, addresses the role of the edge on magnetic behavior uniformity in magnetic nanostructures. The second element, magneto-optical nanostructure spectroscopy, is meant to provide fast and precise individual nanostructure "fingerprints". Another element, microscopy, provides quantitative microstructure and defect information that can be correlated with magnetic behavior. Finally, nanomagnetic modeling element offers an efficient and accurate theoretical predictive tool. 

 

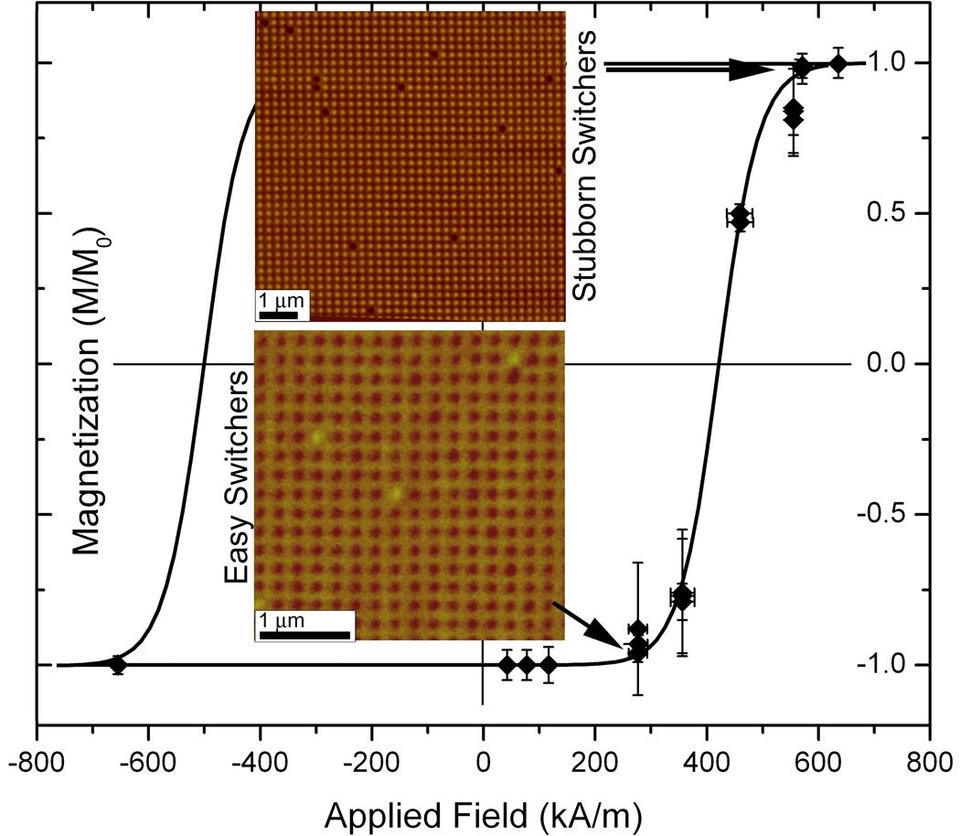
Magnetization reversal in nanodots

Major Accomplishments

Edge roughness on the nanoscale correlates to switching behavior
In this work, we measured the nucleation field, nucleation field distribution, and their dependence on edge roughness in an array of Permalloy magnetic nanostructures. Our two major results are that (1) edge roughness increases the probability for vortex nucleation and thus permits vortices to be stable at larger applied fields, and (2) edge roughness causes broadening of the nucleation-field distribution. We also showed that the nucleation fields, as well as the consistency of those fields among all the nanostructures within the array are sensitive to edge roughness on the order of 1 nanometer.

 

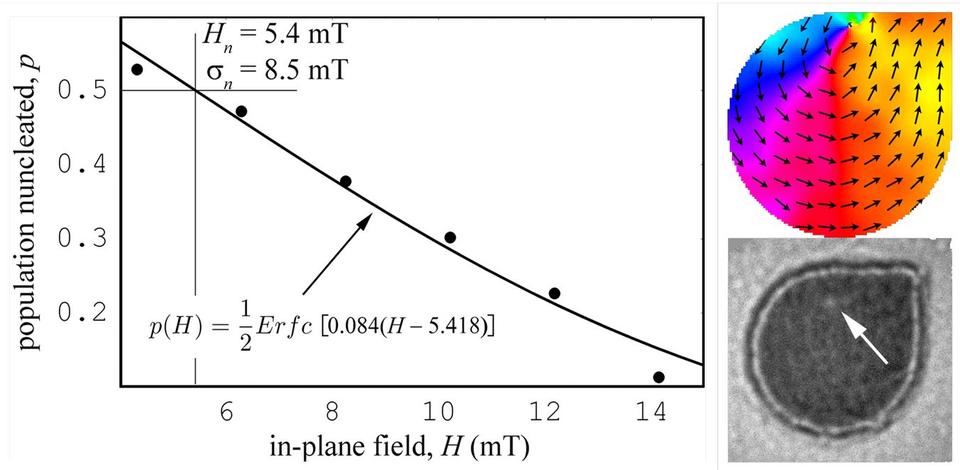
Determining nucleation field in nanostructures

Microstructural origin of switching field distribution
We found an important microstructural origin of switching field distribution (SFD) in polycrystalline Co/Pd nanodot arrays. Based on the evidence that grains with in-plane [100] vectors are correlated to dots with small switching fields, we concluded that these grains "trigger" or initiate switching. Furthermore, the ease of switching these nanodots is linked to the size of the trigger grains. The extent to which the [001] vector points out of plane may also play a role in reducing the switching field. Control of the microstructure, to eliminate the trigger grain, may be the key to reducing the SFD in Co/Pd nanodot arrays.

 

Trigger grain causes SFD in Co/Pd nanodots

Thin film edge magnetic properties varies with patterning process conditions
Using ferromagnetic resonance spectroscopy, we were able to separate edge behavior from "bulk" behavior in Permalloy magnetic nano-stripes. We showed that the patterned edges of magnetic films have measurable magnetic characteristics, and that quantitatively, the magnetic properties depend on the etching conditions used to create the edges. These results have important implications for generating nanostructure arrays with uniform properties and for understanding the behavior of magnetic nano-devices.

 

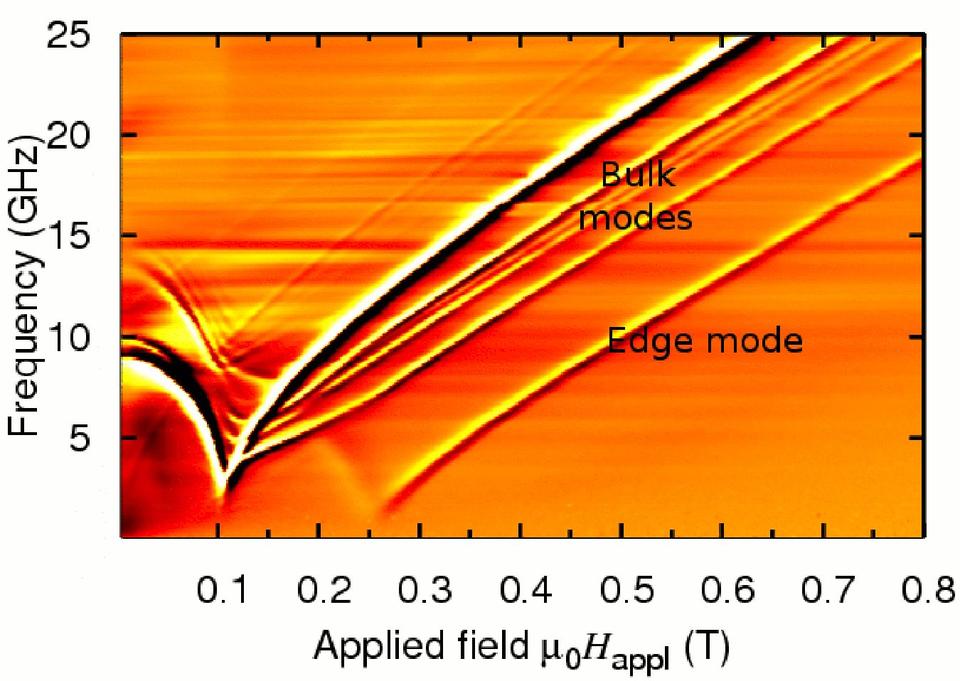
Measured resonances in nanostripes

Micromagnetics on curved geometries using rectangular cells
We introduced a 3-D compatible correction method for calculating the micromagnetics of arbitrary shaped magnetic elements using regular finite-difference discretization. The correction reuses the magnetostatic code on a finer mesh to compute local anisotropy terms for cells in the neighborhood of the boundary. To validate the correction algorithm, we used an edge mode frequency test, which revealed that grid-induced magnetic behaviors were largely eliminated.

 

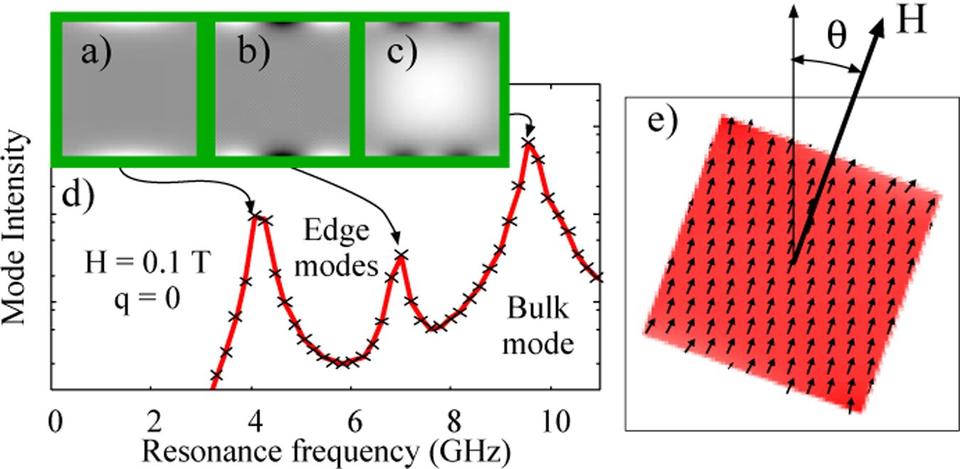
Edge modes test the robustness of correction

Associated Product(s)

Project Summary (PDF)