Fundamental Constants in Nature

Summary

We are involved in efforts to collate data on precision measurements and the theoretical description of these measurements with the aim to improve the values of fundamental constants, such as the fine-structure constant, the electron mass, and the Newtonian constant of gravitation G. These constants are among the best-known constants in the world often reaching relative accuracies of the order of ten significant digits. In fact, the accuracy of many of these constants has improved exponentially in time over the past hundred years. Comparisons of experiment and theory can also be interpreted as a means to find flaws in the standard model of physics. We are also involved in discussions about the measurement concepts “quantity”, “quantity value”, and “unit” in the International System of Units (SI).

The research is performed under auspices of the Task Group on Fundamental Constants, a task group of the Committee on Data for Science and Technology (CODATA). At NIST the research is performed in collaboration with Drs. P. J. Mohr, D. B. Newell, and B. N. Taylor of the Quantum Processes Division.

Description

A schematic diagram of the relationships among constants and measurement tools used to determine the most accurate values for the fine-structure constant α, the electron mass m_e, the Hartree energy E_h, and the atomic mass constant m_u. The constants are constrained by measurements of the energy levels of atomic hydrogen, the g factor of the free electron, the mass of laser-cooled rubidium and cesium atoms, and ratios of atom-to-atom and electron-to-carbon masses.

The Task Group on Fundamental Constants periodically publishes updated evaluations of the fundamental constants of physics and chemistry. These evaluations serve two purposes. First, they provide a self-consistent set of recommended values of the constants for all to use. Second, because they necessitate a summary and analysis of a wide range of experimental and theoretical data, they can identify possible inconsistencies among the data and suggest areas for future work. Scientist all over the world continually improve the accuracy of the fundamental constants.

A constant is only fundamental by convention. For our adjustments, obvious constants are those that appear in basic physical and chemical theory. The Planck constant h, the speed of light in vacuum c, and the elementary charge e are basic quantities in quantum mechanics, general relativity, and quantum electrodynamics. They are exactly defined in the International System of Units (SI). Avogadro’s constant N_A and the Boltzmann constant k are also exact in the SI. The former sets the number of particles in a mole, while the latter connects the Kelvin temperature scale with energies in statistical mechanics and thermodynamics.

Important inexact constants are the Newtonian constant of gravitation G and the dimensionless fine-structure constant α. Masses and magnetic moments of the lightest charged leptons, i.e. the electron and muon, and of light nuclei with charge number Z=0, 1, and 2 also fall within the scope of our work as their precise evaluation often involves knowledge of the fine-structure constant, etc. We provide masses in the SI unit kg and as well as relative atomic masses in the atomic mass unit u (or m_u). The Newtonian constant of gravitation and fine-structure constant are currently known to five and ten significant digits, respectively. The g factor of the free electron and the Rydberg constant are even better known.

Products and ratios of constants, like the vacuum magnetic permeability $$\mu_0=4\pi\alpha\hbar/(e^2c),$$ the molar gas constant R=N_Ak, and the Planck mass $${(\hbar c/G)}^{1/2}$$ have been given dedicated names as they naturally appear in the theoretical description of the quantities observed in the relevant experiments.

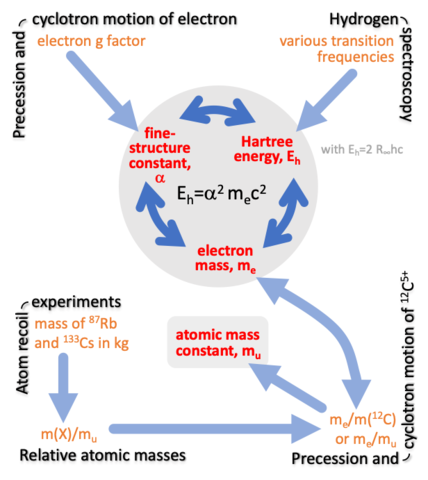
The determination of one constant is often related to the measurement of another. In fact, measurements can give redundant information and used to validate data. The figure on this page describes the role of the equation $$E_\text{H}=\alpha^2m_ec^2$$ in our analysis. It describes the relationship among the Rydberg energy E_H, the fine-structure constant, and the electron mass m_e. Currently, the Rydberg energy is most accurately found from hydrogen and deuterium spectroscopy, while the fine-structure constant is about equally-well found by measuring the g factor of the electron and, surprisingly, measuring the mass of a cesium atom. The mass of the cesium atom is related to the mass of the electron and thus α through the measurement chain shown in the figure.