Atomic Standard for Pressure

Summary

NIST scientists are developing a highly accurate primary standard for pressure in the range 2 MPa to 7 MPa based on fundamental physical properties of helium. With this new standard, we will improve our understanding of piston-cylinder sets used as working pressure standards and we will reduce the uncertainty of their pressure-dependent effective areas.

Description

A quasi-spherical cavity made as a tri-axial ellipsoid. The cavity has three perpendicular axes that are intentionally different by a small amount in order to split the degenerate microwave modes.

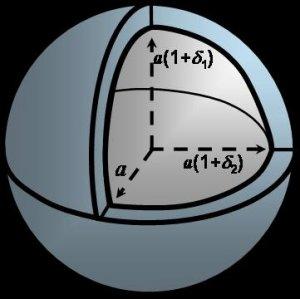
Atomic physicists have calculated the pressure p(n,T) of helium gas as a function of the gas's temperature T and its refractive index at microwave frequencies, n. Near room temperature and 4 MPa, the fractional uncertainties from the calculations, the impurities in helium, state-of-art measurements of the temperature, refractive index, and the deformation of the apparatus under pressure are approximately 6.2 parts per million. The combination of these uncertainties is smaller than the uncertainties of existing pressure standards (piston gages) near 4 MPa. Therefore, the refractive index of helium can become an atomic standard of pressure to calibrate piston-cylinder sets. Calibrations will become easier after we compare the index of refraction of helium n_He(p,T) to the index of refraction of argon n_Ar(p,T) with uncertainties equivalent to 1×10⁻⁶p. After the helium-argon comparison, argon will be a secondary atomic standard of pressure. An argon standard will have 1/8th the sensitivity to deformation of the apparatus and 1/8th the sensitivity to water impurities because [n_Ar(p,T) − 1]/[n_He(p,T) − 1] ≈ 8.

Above 300 kPa, NIST's pressure standards are commercially manufactured piston-cylinder sets. In operation, both the piston and the cylinder deform significantly with pressure and the piston rotates continuously to insure gas lubrication. Because of these complications, piston-cylinder sets are calibrated using NIST's primary-standard mercury manometer below 300 kPa and the calibration is extrapolated to higher pressures using numerical models of the coupled gas flow and elastic distortions. The data used for extrapolation exhibit poorly understood dependencies on the gas used and its flow rate; therefore, the extrapolation is not fully trusted. The extrapolation cannot be checked with existing technologies; however, the atomic standard of pressure will reduce extrapolation uncertainties.

Apparatus for comparing the refractive index of argon n_Ar to the calculated refractive index of helium n_He. Two quasi-spherical, gas-filled cavities are shown inside pressure-controlled vessels that are contained in the same temperature-controlled bath. We measure the frequencies f and half-widths g of the microwave resonances of both gas-filled cavities at the same temperature and pressure. The cavities shrink under hydrostatic pressure; however, their isothermal compressibility κ_T cancels out of the ratio n_Ar/n_He.

Major Accomplishments

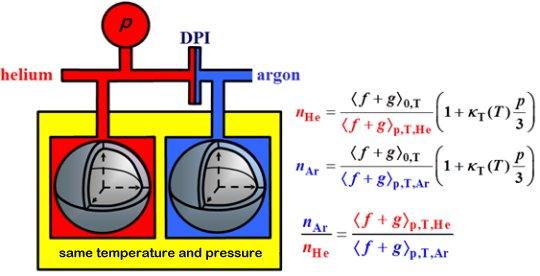
1. Initially, we built cross capacitors to measure the dielectric constant ε of helium as the basis of a pressure standard p(ε,T). [1] The dielectric constant measurements were limited by the linearity and resolution of commercially-manufactured capacitance bridges. This led us to replace dielectric constant measurements with higher-resolution refractive index measurements obtained from the microwave resonance frequencies of helium-filled, quasi-spherical cavities invented at NIST. [2]
2. We measured the fractional difference (p_piston/p_atomic − 1) = (1.8±9.1)×10⁻⁶ between the pressure determined from NIST's piston-cylinder standards and the atomic standard [n_He(p,T)] in the pressure range 0.14 MPa to 7 MPa at the temperature of the triple point of water, T_W = 273.16 K. [3]
3. We measured the ratios [n_Ar(p,T) − 1]/[n_He(p,T) − 1] with a fractional uncertainty of 2.5×10⁻⁶ at the triple points of mercury (T_Hg = 234.3156 K), water (T_W = 273.16 K), and gallium (T_Ga = 302.9146 K). [4]

For more information, contact James Schmidt.