Magnetic Monopoles and Spin Liquids
From the symmetry of Maxwell's equations of electromagnetism, as well as field theoretical arguments, magnetic charges or monopoles would be expected to exist and produce magnetic fields, and moving magnetic monopoles electric fields. But no magnetic monopoles have ever been observed despite longstanding experimental searches1 since the hypothesis of the Dirac monopole2. Recently, attention has turned to condensed matter systems where tractable analogs of magnetic monopoles might be found, and one prediction3 is for an emergent elementary excitation in the spin ice compound Dy2Ti2O7. 'Spin Ice' is a special magnetic system where the Dy spins occupy a cubic pyrochlore lattice, which is a corner sharing network of tetrahedra with the spins located at the vertices of the tetrahedra (see figure below). The magnetic anisotropy requires the spins to point along a line to the center of the tetrahedron, either parallel or antiparallel, while neighboring spins interact via an effective ferromagnetic coupling. The interactions between all the spins in the system cannot be optimized simultaneously, making the magnetic spins 'frustrated', and preventing a conventional ordered magnetic state to form even at the very lowest temperatures achievable. Instead of a conventional ground state with long range magnetic order, the lowest energy spin configurations on each tetrahedron follow the ice rule, in which two spins point inward and two point outward on each tetrahedron. This "2-in & 2-out" ground state spin structure has a six-fold degeneracy (see Figure below), and the possible ground states of the entire tetrahedral network are macroscopically degenerate in the same way as the famous example of disordered protons in H2O ice. In solid water, the protons are disordered even at absolute zero temperature and thus retain finite entropy, and the same disordered ground state occurs for the magnetic moments in Dy2Ti2O7,--hence the name 'Spin Ice'.
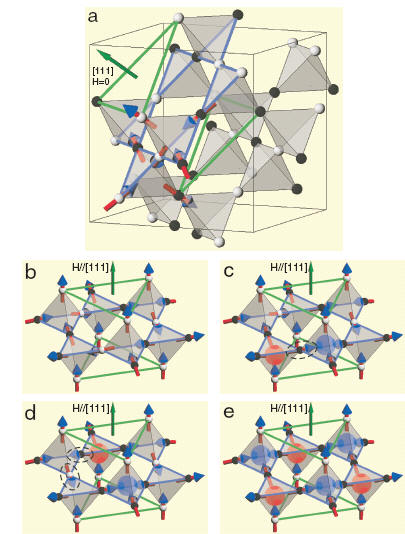
Illustration of spin ice, kagome ice and magnetic monopoles. a, Magnetic moments (spins) of Dy in Dy2Ti2O7 reside on the corners of tetrahedra of the cubic pyrochlore lattice. They are represented by arrows pointing inward or outward from centers of the tetrahedra, depicted equivalently by black and white spheres. At low temperatures, four magnetic moments on each tetrahedron obey the ice rule, two spins pointing into each tetrahedron and two pointing out (2-in and 2-out structure) to minimize the effective ferromagnetic interaction between neighboring spins. The resulting spin ice state consists of a macroscopic number of disordered configurations, an example of which is shown in a above. The pyrochlore lattice consists of stacked triangular and kagome lattices, shown by green and blue lines, respectively, along a [111] direction. (b) Under small [111] magnetic fields, spins on the kagome lattice remain in the disordered kagome ice state. (c) An excited state is induced by flipping a spin from (b), enclosed by a dashed circle, where neighboring tetrahedra have 3-in, 1-out and 1-in, 3-out configurations. These ice-rule-breaking tetrahedra are represented by magnetic monopoles with opposite charges depicted by spheres. (d) By consecutively flipping two spins from (c), the monopoles are fractionalized. (e) As the magnetic field is increased, H >> Hc, spins realize a fully ordered, staggered arrangement of monopoles.
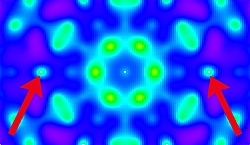
Neutron scattering research has detected the equivalent of "magnetic monopoles" in a low temperature condensed matter magnetic system called 'spin ice'. These monopoles are analogs to the elusive magnetic monopole particles theorized in 1931 by Paul Dirac - but never actually found. The red arrows locate the scattering associated with the creation of magnetic monopoles.
In addition to this remarkable behavior, it has been recently theorized3 that the excitations from these highly degenerate ground states are topological in nature and mathematically equivalent to magnetic monopoles. We have carried out neutron scattering experiments that confirm the existence of monopoles in spin ice, and that they interact via the magnetic Coulomb force.4 The establishment of magnetic monopoles in this condensed matter system represents a fundamentally new type of collective excitation, and opens the door for studies of aspects of magnetic monopoles that include pair creation and interaction, individual motion, correlations, and cooperative phenomena.
These cubic pyrochlore materials, with their competing interactions and magnetic frustration, exhibit many other interesting emergent properties. Including the quantum spin fluctuations inherent at these very low temperatures ( < 1 K), no magnetic order at all may occur, leading to a hidden order state of electric quadrupole moments, neighboring a spin liquid that is likely a U(1) quantum spin liquid state.5,6,7
1. For a review, see K. A. Milton, Theoretical and experimental status of magnetic monopoles. Rep. Prog. Phys. 69, 1637-1712 (2006).
2. P. A. M. Dirac, Quantised singularities in the electromagnetic field, Proc. R. Soc. A 133, 60-72 (1931).
3. Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42-45 (2008).
4. Observation of Magnetic Monopoles in Spin Ice, Hiroaki Kadowaki, Naohiro Doi, Yuji Aoki, Yoshikazu Tabata, Taku J. Sato, J. W. Lynn, K. Matsuhira, and Z. Hiroi, J. Phys. Soc. Japan 78, 103706 (2009).
5. Quantum Spin Fluctuations in the Spin Liquid State of Tb2Ti2O7, Hiroshi Takatsu, Hiroaki Kadowaki, Taku J. Sato, Jeffrey W. Lynn, Yoshikazu Tabata, Terno Yamakaki, and Kazuyuki Matsuhira, J. Phys. Cond. Matr. 24, 052201 (2012).
6. Quadrupole Order in the Frustrated Pyrochlore Tb2+xTi2−xO7+y, H. Takatsu, S. Onoda, S. Kittaka, A. Kasahara, Y. Kono, T. Sakakibara, Y. Kato, B. Fåk, J. Ollivier, J. W. Lynn, T. Taniguchi, M. Wakita, and H. Kadowaki, Phys. Rev. Lett. 116, 217201 (2016). Erratum: Phys. Rev. Lett. 127, 069902(E) (2021).
7. Quantum Critical Point in the Sc-doped Itinerant Antiferromagnetic TiAu, E. Svanidze, T. Besara, J. K. Wang, D. Geiger, L. Prochaska, J. Santiago, J. W. Lynn, S. Paschen, T. Siegrist, and E. Morosan, Phys. Rev. B 95, 220405(R) (2017).
8. Phase Diagram of a-RuCl3 in an in-plane Magnetic Field, J. A. Sears, Y. Zhao, Z. Xu, J. W. Lynn, and Young-June Kim, Phys. Rev. B 95, 180411(R) (2017).
9. Spin correlations of quantum-spin-liquid and quadrupole-ordered states of Tb2+xTi2-xO7+y, Hiroaki Kadowaki, Mika Wakita, Björn Fåk, Jacques Ollivier, Seiko Ohira-Kawamura, Kenji M Kofu-Nakajima, and Jeffrey W. Lynn, Phys. Rev. B 99, 014406 (2019).
10. Absence of Magnetic Order in the Spin Liquid Candidate Ca3Cu2GeV2O12, Joey A. Lussier, Brooke Richtik, Cole Mauws, Jeffrey W. Lynn, and Chris R. Wiebe, J. Phys.: Condens. Matter 32, 134001 (2020).
11. Materializing Rival Ground States in the Barlowite Family of Kagome Magnets: Quantum Spin Liquid, Spin Ordered, and Valence Bond Crystal States, Rebecca W. Smaha, Wei He, Jack Mingde Jiang, Jiajia Wen, Yi-Fan Jiang, John P. Sheckelton, Charles J. Titus, Suyin Grass Wang, Yu-Sheng Chen, Simon J. Teat, Adam A. Aczel, Yang Zhao, Guangyong Xu, Jeffrey W. Lynn, Hong-Chen Jiang and Young S. Lee, Nature Partner Journals: Quantum Materials 5, 23 (2020).
12. Phase Diagram of YbZnGaO4 in Applied Magnetic Field, William Steinhardt, P. A. Maksimov, Sachith Dissanayake, Zhenzhong Shi, Nicholas Butch, David Graf, Andrey Podlesnyak, Yaohua Liu, Yang Zhao, Guangyong Xu, Jeffrey W. Lynn, Casey Marjerrison, A. L. Chernyshev, and Sara Haravifard, Nature Partner Journals Quantum Materials 6, 78 (2021)
13. Universal Dynamics of Magnetic Monopoles in Two-dimensional Kagome Ice, Hiroshi Takatsu, Kazuki Goto, Taku J. Sato, Jeffrey W. Lynn, Kazuyuki Matsubayashi, Yoshiya Uwatoko, Ryuji Higashinaka, Kazuyuki Matsuhira, Zenji Hiroi, and Hiroaki Kadowaki, J. Phys. Soc. Jpn. 90, 123705 (2021).
14. Magnetic ground state of the Kitaev Na2Co2TeO6 spin liquid candidate, Weiliang Yao, Yang Zhao, Yiming Qiu, Christian Balz, J. Ross Stewart, Jeffrey W. Lynn, and Yuan Li, Phys. Rev. Research 5, L022045 (2023).
__________________________________________________
See the Invited Talk (C9.2) entitled "Observation of Magnetic Monopoles in the Spin Ice Dy2Ti2O7" presented at the International Conference on Neutron Scattering (May, 2009).
An article about the work is available at 2Physics.com:
in the November 2009 archives of 'Condensed Matter' or 'Elementary Particles'.
For a popular account, see
NIST Tech Beat
http://www.nist.gov/ncnr/monopole_100609.cfm


