U.S. flag

An official website of the United States government

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.

Material Measurement Laboratory / Chemical Sciences Division

Chemical Informatics Group

TMMC: Reference Adsorption Isotherms for CO2 in Metal-organic Frameworks

Share

Grand-canonical Transition-Matrix Monte Carlo (GC-TMMC) simulations [1, 5-10] of CO2 were performed at T = 300 K and 350 K in four metal-organic frameworks (MOFs). The particle number range was divided into windows advanced trial moves were performed to ensure adequate sampling at high densities. The main result of a GC-TMMC simulation is the particle number probability distribution (PNPD), which is constructed by stitching together the particle number distributions from each window. The adsorption isotherm may be determined from the PNPD [10]. At each value of N, average total potential energies U were collected and these quantities were used to compute the isosteric heat of adsorption.

Simulations used different combinations of Monte Carlo moves depending on the number of particles, as described below. Low density windows used a conventional set of moves (i.e., no configurational bias) whereas high density windows used a configurational bias strategy known as Dual-cut configurational bias (DCCB) Monte Carlo [13]. Additionally, low-density windows started in Wang-Landau biasing mode to quickly generate a guess of the PNPD, later switching to TMMC mode; data from the TMMC phase of the simulation was saved and reported here.

All simulations were performed using the open-source FEASST Monte Carlo engine [14], version v0.19.0 (commit hash 31d57778245ef6784931d2422e851c6d77a14a64).

Other key simulation details common to all simulations are given below:

Fluid Model TraPPE CO2[11]
Lennard-Jones cutoff 12A, with linear-force shift tail
Ewald Parameters Set according to DL_POLY recipe [15], with relative tolerance 10-5

Standard Move Set
   (N < 100)

Translation, weight 0.3
Rotation, weight 0.2
Insertion/Deletion, weight 0.4
Advanced Move Set
   (N ≥ 100)		 Translation, weight 0.1
DCCB Regrowth (single Oxygen), weight 0.06
DCCB Regrowth (both Oxygens), weight 0.04
DCCB Growth (full CO2 particle), weight 0.8
DCCB Details

Number of trials per atom: 4
Reference Potential: Lennard-Jones + Ewald Realspace
Cutoff Radius for Reference Potential: 6A
Total MC Trials 1.0e8
Bias update freq 1.0e4
Physical Parameters CODATA 2018 [12]

The adsorbent MOFs were reconstructed from publicly-available crystal structures and replicated to ensure that the simulation cell was at least twice the cutoff radius in all dimensions. Forcefields for each MOF were taken from published literature. The MOF structure and forcefield are provided in FEASST particle files in the data repository associated with this page (see "Data Availability" below). Coulombic interactions were handled using the Ewald summation method [2,3] (parameters listed in the metadata files). Lorentz-Berthelot mixing rules were used to set the unlike-atom Lennard-Jones parameters.

Simulation details specific to each MOF 

  ZIF-8 CuBTC UiO-66 IRMOF-1
Number of Windows 48 32 64 32
Nmax 300 210 480 235
Unit Cell Replication (Nx, Ny, Nz) (2,2,2) (1,1,1) (2,2,2) (1,1,1)
Cubic Box Dimensions (A) 34.023240 26.3430 41.40080 25.6690
Simulation MOF Mass (amu) 21846.91 9677.91 53249.82 6158.94
MOF Forcefield,
Reference		 Snurr [16] Calero IV [17] Snurr [18] DREIDING [19] + m-CBAC [20]
FEASST MOF Particle data.ZIF8_Snurr_rep222 data.CuBTC_CaleroIV_rep111 data.UiO66_Snurr_rep222 data.IRMOF1_mCBAC_rep111

Note: all four MOFs have cubic unit cells

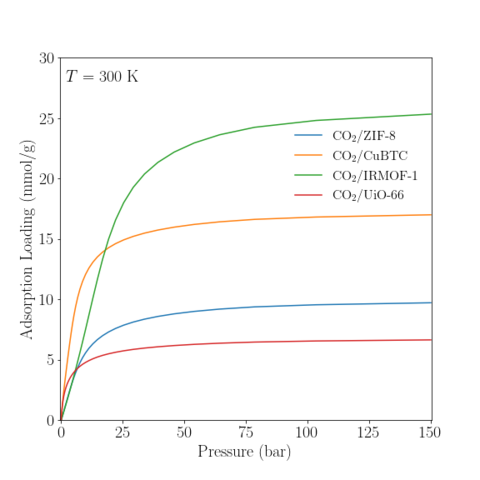
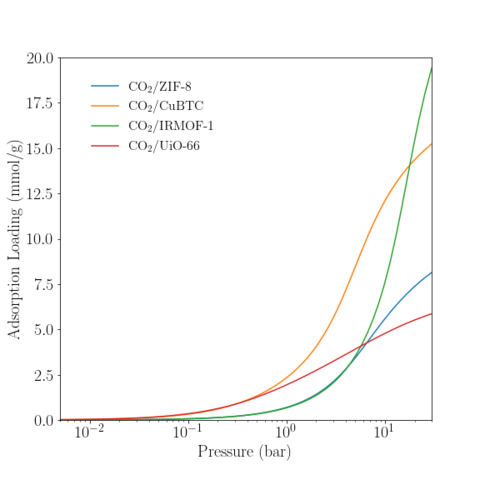
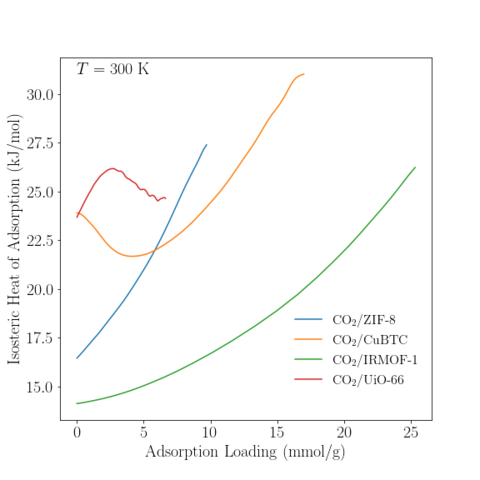
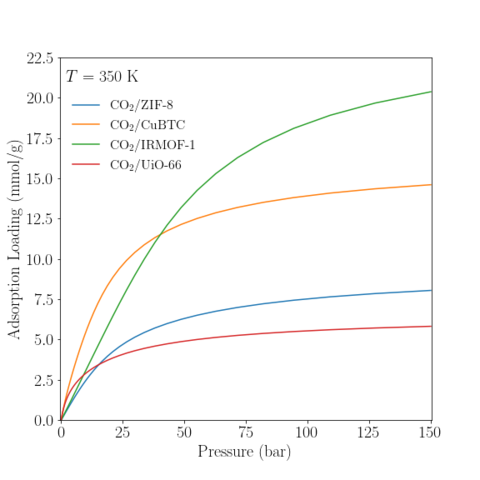
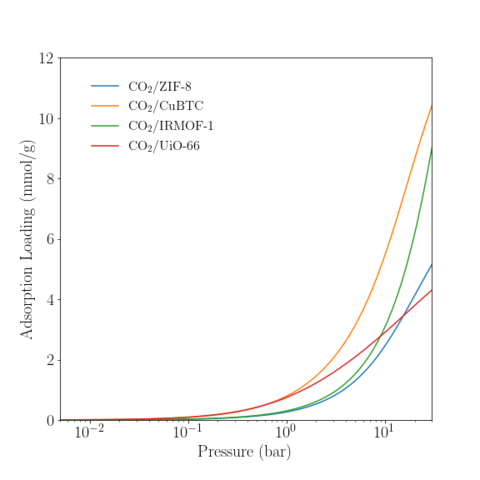
The result of each simulation is the PNPD and average potential energy (for each N state). The PNPD may be used to compute the adsorption isotherm by the histogram-reweighting procedure described by Siderius and Shen [10]. All systems were single phase and, hence, no phase decomposition of the PNPD was necessary. The pressure for a particular chemical potential was determined from GC-TMMC simulation of the bulk CO2 fluid [4]; the PNPD and average potential energy of the bulk fluid are also provided in the associated data repository.

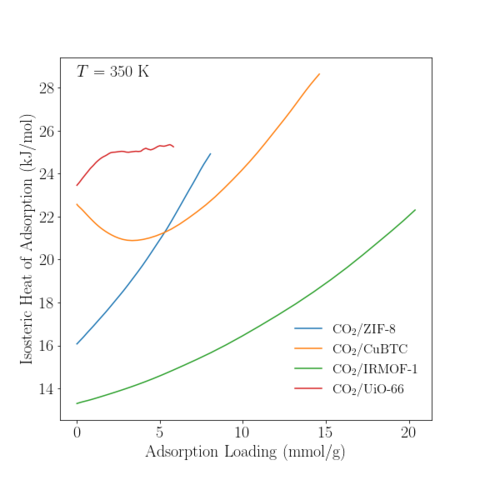
The isosteric heat of adsorption was computed as

$$ q_{st} = k_B T -\dfrac{<UN>-<U><N>}{<N^2> - <N>^2}$$

The <...> brackets indicate grand-canonical averages

Results

Temperature = 300K

Reference adsorption isotherm of CO2 in various MOFs at 300K
Adsorption Isotherms of CO2 in four MOFs at 300 K.
Low-pressure Reference adsorption isotherm of CO2 in various MOFs at 300 K
Low-pressure region of isotherms at 300 K.
Isosteric Heat of Adsorption for CO2 in various MOFs at 300 K
Isosteric Heat of Adsorption (qst) for CO2 in various MOFs at 300 K

Temperature = 350 K

Reference adsorption isotherm of CO2 in various MOFs at 350K
Adsorption Isotherms of CO2 in four MOFs at 350 K.
Low-pressure Reference adsorption isotherm of CO2 in various MOFs at 350 K
Low-pressure region of isotherms at 350 K.
Isosteric Heat of Adsorption for CO2 in various MOFs at 350 K
Isosteric Heat of Adsorption (qst) for CO2 in various MOFs at 350 K

Data Availability

Various data files used to generate the reference isotherms are available in a Git Repository: https://github.com/dwsideriusNIST/NIST_SRSW_Data/tree/master/CO2_REF_ISOTHERMS

Files in the repository include:
FEASST particle files for the MOF materials [includes atomic coordinates and the forcefield parameters]
FEASST particle file for TraPPE CO2
Particle number probability distributions and canonical energy averages for both the bulk and adsorbed CO2
Isotherm data files, including the adsorption isotherm and isosteric heat and estimated uncertainties, formatted as AIF files [22]

References

  1. J. R. Errington, J. Chem. Phys. 118, 9915 (2003).
  2. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids (Oxford University Press, New York, 1989).
  3. D. Frenkel and B. Smit, Understanding Molecular Simulation, 2nd ed. (Academic, San Diego, 2002)., pp.37-38.
  4. J. R. Errington and A. Z. Panagiotopoulos, J. Chem. Phys., 109, 1093 (1998).
  5. J. R. Errington and V. K. Shen, J. Chem. Phys., 123, 164103 (2005).
  6. V. K. Shen and D. W. Siderius, J. Chem. Phys., 140, 244106, 2014.
  7. V. K. Shen and J. R. Errington, JPC B 108, 19595, 2004.
  8. V. K. Shen and J. R. Errington, JCP 122, 064508, 2005.
  9. V. K. Shen, R. D. Mountain, and J. R. Errington, JPC B 111, 6198, 2007.
  10. D. W. Siderius and V. K. Shen, JPC C 117, 5681, 2013.
  11. J. A. Potoff and J. I. Siepmann, AIChE J., 47, 1676–1682, 2001.
  12. CODATA Internationally recommended 2018 values of the Fundamental Physical Constants
  13. T. J. H. Vlugt, M. G. Martin, B. Smit, J. I. Siepmann, and R. Krishna, Mol Phys, 94, 727, 1998.

  14. H. W. Hatch, N. A. Mahynski, and V. K. Shen J Res Natl Inst Stan, 123, 123004, 2018.

  15. E. I. Todorov and W. Smith, The DL\_POLY User Manual (version 4.03).

  16. H. Zhang and R. Q. Snurr, JPC C, 121, 24000, 2017.

  17. J. M. Castillo, T. J. H. Vlugt, and S. Calero, JPC C 112, 15934, 2008.

  18. P. Ghosh, Y. J. Colón, and R. Q. Snurr, Chem Commun, 50, 11329, 2014.

  19. S. L. Mayo, B.D. Olafson and W. A. Goddard, JPC, 26, 8897, 1990.

  20. C. Zou, D. R. Penley, E. H. Cho, and L-C. Lin, JPC C 124, 11428, 2020.

  21. J. D. Evans, V. Bon, I. Senkovska, S. Kaskel, Langmuir, 37, 4222, 2021.

Chemistry, Chemical engineering and processing, Chemical thermodynamics and chemical properties, Theoretical chemistry and modeling, Thermochemical properties, Materials, Modeling and computational material science, Metrology, Standards and Reference data
Created September 28, 2022, Updated August 17, 2023