IRMOF-2: Effect of Partial Charge Method on Adsorption Thermodynamics
A sequence of computational methods were used to examine the affect of partial charge calculation method on simulated adsorption properties of IRMOF-2. First, the electronic structure of IRMOF-2 was computed. Second, the electron density map yielded partial charges from various calculation methods. Lastly, Monte Carlo molecular simulations were performed to obtain the adsorption isotherms of CO2 in IRMOF-2.
Electronic Structure Calculation and Partial Charge Methods
The structure and electron density of IRMOF-2 were converged and computed, beginning with a sample IRMOF-2 structure [1,2], using the open-source Quantum ESPRESSO electronic structure calculator [3,4]. Partial charges for IRMOF-2 were then derived from the converged electron density maps. Parameters for the density-functional theory and partial charge calculations are as follows:
| Software Package | Quantum ESPRESSO, v5.0.2 [3,4] |
| Pseudopotential / Plane Wave Basis Set | pbe-mt_fhi [5] |
| Kinetic Energy Cutoffs: | |
| Wavefunction | 80 Ry |
| Charge Density and Potential | 320 Ry |
| Self-consistent Energy Convergence Threshold | 1.0E-07 Ry |
| Converged Cubic Lattice Constant | 25.7718 Å |
| Partial Charge Methods & Software | 1. Bader Charge Analysis [6]; Bader Charge Analysis code [7] 2. Löwdin Population Analysis [8]; Quantum Espresso projwfc.x [9] 3. Voronoi Partitioning [10]; Bader Charge Analysis code [7] |
Density function theory calculations were carried out using the pbe-mt_fhi pseudopotential, which is a non-relativistic norm-conserving pseudopotential created using the Martins-Troullier method and makes use of the Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional.
Lattice constants (i.e., unit cell dimensions) were optimized using damped (Beeman) dynamics of the Wentzcovitch extended Lagrangian with a Wmass (fictitious mass) value of 0.0001 and a convergence threshold on the pressure of 0.05 kbar.
Data Download:
Gaussian Cube Data for Converged Electron Density Map (Download Link Coming Soon):
irmof2.density.cube.gz
XYZ-formatted Structure and Charges (Download Links Coming Soon):
irmof2.structure_charges.Bader.xyz
irmof2.structure_charges.Lowdin.xyz
irmof2.structure_charges.Voronoi.xyz
The XYZ files listed above are modified from but are compatible with the standard XYZ format. In the file, the first line gives the number of atoms in the file. The second line lists the cubic cell dimensions in Å. In the remaining lines, the first column lists the atom type and the second through fourth columns give the Cartesian coordinates of the atom in Å, as is standard for XYZ files. The fifth column provides the partial charge of that atom, in e (the elementary charge, 1.602176565E-19 coulombs), as derived using the partial charge methods listed above. We note that the partial charges in column five may not sum to zero. Consequently, the sixth column lists adjusted partial charges, where some of the atoms have a small amount of charge added or subtracted to neutralize the charge of the material.
Monte Carlo Molecular Simulations
The adsorption of CO2 by IRMOF-2 was modeled via Monte Carlo molecular simulations, using an existing force field of CO2, a generic force field for the interaction between the gas and IRMOF-2 structure, and the partial charges obtained as described above.
Fluid Simulation Parameters:
The CO2 adsorbate fluid was modeled via the TraPPE force field [11], which models CO2 as a rigid triatomic molecule with Lennard-Jones sites and partial charges at each atom. The Lennard-Jones parameters and partial charges for TraPPE CO2 are:
| Atomic Species | σ (Å) | ε/kB (K) | q (e) |
| C | 2.8000 | 27.0000 | 0.7000 |
| O | 3.0500 | 79.0000 | -0.3500 |
IRMOF-2 Material Simulation Parameters:
The constituent atoms in IRMOF-2 were modeled using the generic DREIDING force field [12]. Each atom has a Lennard-Jones site and partial charge, with parameters given by:
| Atomic Species | σ (Å) | ε/kB (K) |
| Zn | 4.0440 | 27.6950 |
| C | 3.4729 | 78.8880 |
| O | 3.0332 | 48.1900 |
| H | 2.8464 | 7.6520 |
| Br | 3.5190 | 186.3150 |
Cross terms were computed using standard Lorentz-Berthelot mixing rules:
| $$ \Large \sigma_{ij} = \dfrac{\sigma_i + \sigma_j}{2} $$ | $$ \Large \epsilon_{ij} = \sqrt { \epsilon_i \epsilon_j} $$ |
Simulation Run Information:
Adsorption simulations were run using the Transition-matrix Monte Carlo technique and the simulation results were analyzed using histogram-reweighting [13] and the method described in Ref. [14]. The equation of state of CO2 was obtained from bulk simulations of TraPPE CO2 as described in "Benchmark results for TraPPE Carbon Dioxide" in the NIST Standard Reference Simulation Website. Parameters for the simulations were:
| METHOD | Grand-canonical transition-matrix Monte Carlo and histogram re-weighting [13,14] |
| Fluid | Carbon Dioxide |
| Model | TraPPE [11] |
| TRUNCATION | |
| Lennard-Jones | 12 Å + Linear Force Shift |
| Electrostatics | 12 Å + Ewald Summation |
| Probability of Displacement. Move | 0.3 |
| Probability of Rotation Move | 0.2 |
| Probability of Insert/Delete Move | 0.5 |
| Biasing Function Update Frequency | 1.0E6 trial moves |
| Simulation Length | 1.0E9 trial moves |
| Imposed Temperature | 303K |
| Imposed Chemical Potential | -136.0 εCC |
| Equivalent Pressure | 111.8 bar |
| Simulation Cell Side Length | 25.7718 Å |
| Simulation Cell Volume (1 Unit Cell) | 17117.260 Å3 |
| Accessible Volume Fraction | 0.4738180 |
| Minimum number of CO2 Molecules | 0 |
| Maximum number of CO2 Molecules | |
| Bader | 240 |
| Löwdin | 240 |
| Voronoi | 240 |
Results:
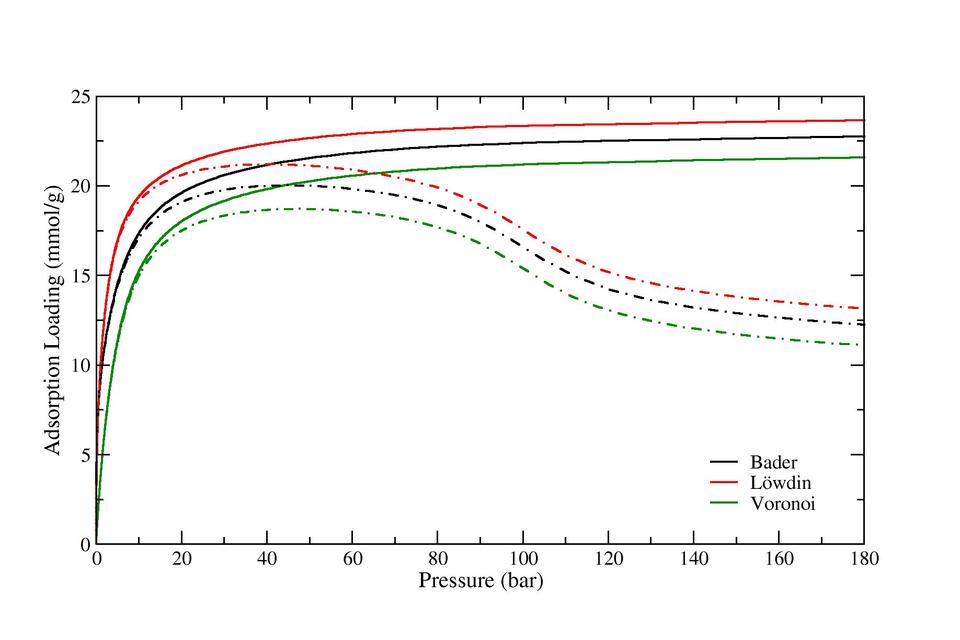
Figure 1: Adsorption Isotherms of Carbon Dioxide in IRMOF-2 at 303K, computed using GC-TMMC molecular simulations with the simulation parameters given above and the partial charge calculation scheme noted in the figure. Solid lines are the absolute adsorption given in millimoles of adsorbate per gram adsorbate. Dot-dashed lines are the excess adsorption, computed using the Accessible Volume definition.
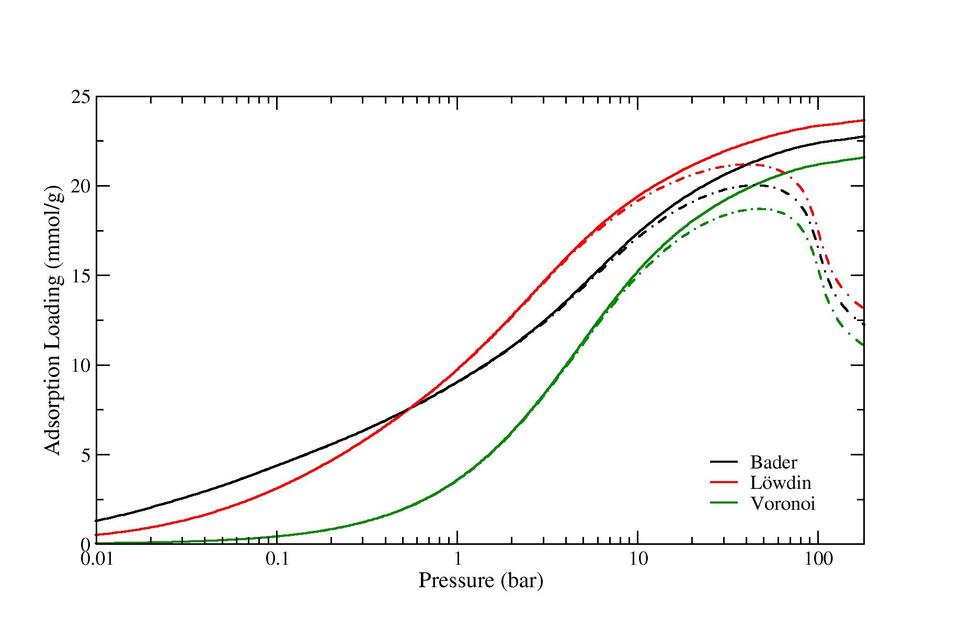
Figure 2: As for Figure 1, plotted in semi-logarithmic form.
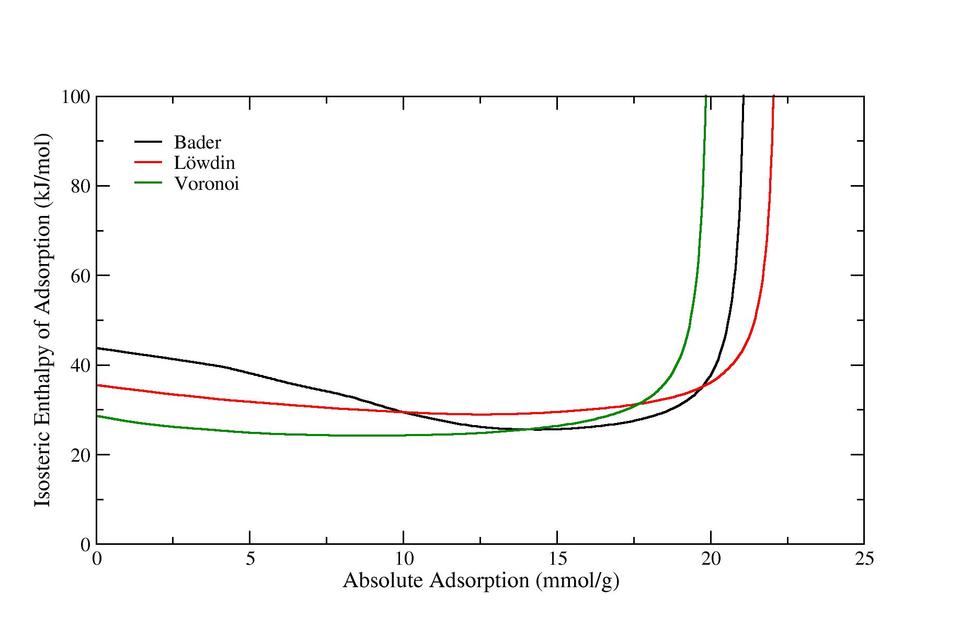
Figure 3: Isosteric Enthalpy of Adsorption of Carbon Dioxide adsorbed in IRMOF-2, computed from GC-TMMC molecular simulations using the method described by Siderius and Shen [14].
- M. Eddaoudi et al., Science, 295, 469-472, (2002).
- https://utkstair.org/clausius/docs/atoms/explosivesensors/index.html; Provides XYZ-formatted structures of select IRMOF materials described by Eddaoudi et al. in Ref. 1, Accessed September 18, 2014.
- P. Giannozi et al., J. Phys.: Condens. Matter, 21, 395502, (2009).
- Quantum ESPRESSO, https://www.quantum-espresso.org, Accessed September 18, 2014.
- Quantum ESPRESSO Pseudopotentials https://www.quantum-ESPRESSO, accessed September 18, 2014.
- R. F. Bader, Atoms in Molecules: A Quantum Theory, (Oxford University Press, Oxford, 1990).
- G. Henkelman, A. Arnaldsson, and H., Comp. Mat. Sci., 36, 354-360, (2006).
- P. O. Löwdin, Adv. Quantum Chem., 5, 185-1999, (1970).
- Quantum ESPRESSO projwfc.x, Accessed September 18, 2014.
- P. Politzer and R. R. Harris, J. Am. Chem. Soc., 92, 6451-6454, (1970).
- J. J. Potoff and J. I. Siepmann, AIChE J., 47, 1676–1682 (2001).
- S. L. Mayo, B. D. Olafson, and W. A. Goddard III, J. Phys. Chem., 94, 8897-8909, (1990).
- J. R. Errington, J. Chem. Phys. 118, 9915 (2003).
- D. W. Siderius and V. K. Shen, J. Phys. Chem. C, 117, 5861-5872 (2013).

