Quantum Information: Changing the Rules of the Game

I was a math researcher at the University of Michigan back in 2008 when I had the crazy—one could even say random—notion to shift from studying pure mathematics to studying quantum information science.

My mentor at the time was confused by this. Why give up the field in which you have all your training and switch to something you don’t know? My short answer is that math is both an art and a tool. I had seen the artistic side and now I wanted to put math to use. Perhaps more importantly, though, quantum information just seemed cool. It was a young field, it had gotten attention in popular science media, and the underlying mathematics was really interesting.

This was more than just a shift in subject matter. Pure mathematicians are used to fixed rules, untroubled by the messiness and uncertainty of everyday experience. We set down "axioms," which are fixed assumptions, and then we build "theorems," which are deductions we make from those assumptions. A "proof" is a final—and immutable—certification of the truth of a theorem.

In information science, however, this is not so. And that is a fact that affects us every day.

Each time I do a credit card transaction online, I am assuming that a certain cryptographic protocol will successfully hide my information well enough to prevent criminals from stealing my credit card number and going on a shopping spree. Assumptions like this can be “proved” in a sense, but those kinds of proofs are based on a foundation that may have to be revised over time because of developments in other fields. This is part of what makes information theory so challenging, and what makes it so much fun.

Quantum Logic

In the early 20th century, physicists found things going on at the subatomic level that were very hard to explain. Basic ideas of what it means to be in a “position” and “state” were called into question.

In my everyday life, I can put my car key on the kitchen counter, or I can leave it in my pocket, but I can't do both. I may forget where I put it afterward, but unless one of my cats got to it, it's still in one place or the other.

At the subatomic scale, things are … different. A key that behaved according to quantum rules could be both in my pocket and on the counter at the same time. And when I check to see where it is, it would randomly end up in one location or the other. This is the idea of quantum superposition, and it was eventually decided that, as strange as it seems, this concept provides the right way to explain the results of certain experiments.

Going further, two particles can be linked, or “entangled,” in a superposed state, which means that observations of the two will always agree, no matter how far apart they happen to be.

Now, here’s an example to illustrate why we need to pay attention to “quantum logic.” Below you see a math puzzle called the "Magic Square game." It's the kind of problem that might have shown up in an early round of math competitions that I used to do.

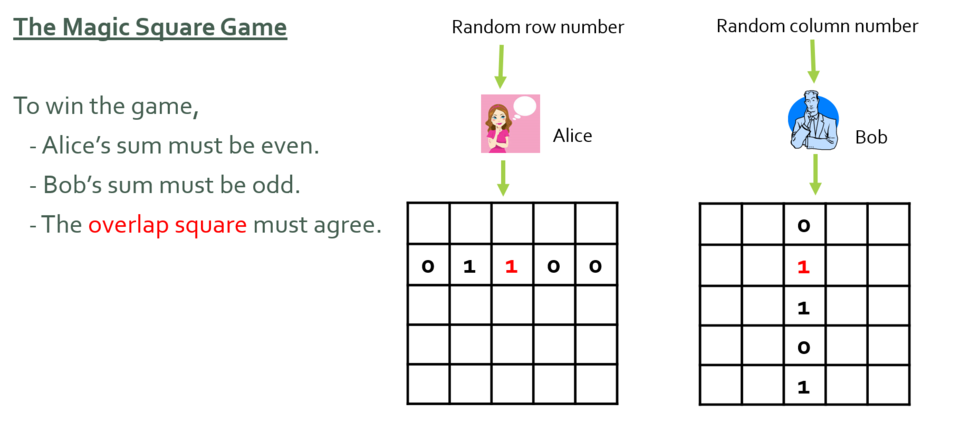
Alice, who is assigned a random row, and Bob, who is assigned a random column, each has to fill in boxes in a grid that satisfy all three of the given conditions. Most importantly, they can't communicate while the game is underway. Is there a strategy that will allow them to win this game every time? (In the example shown, they have won, but maybe they just got lucky.)

We can imagine Alice and Bob trying to work out a script in advance. Here’s an attempt:

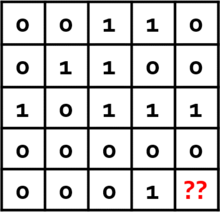
This strategy is good (rows are even, columns are odd) except that there is no way to correctly fill in the last square. And if you try starting over and filling in the grid in a different way, you’ll find that you always run into a similar snag.

With a short argument, we can convince ourselves that the Magic Square puzzle has no solution. In any script, Alice will find that since each of her rows must sum to an even number, her entire script must sum to an even number. Bob’s columns, on the other hand, must sum to an odd number, so his entire script must sum to an odd number! Since their scripts cannot agree, they don't have a perfect strategy.

The Magic Square game is impossible to win. Or is it?

If we allow Alice and Bob to share entangled particles, the scenario changes. Quantum information is not governed by ordinary probability theory, which is based on real numbers, but by linear operators, which are rectangular arrays of numbers. Linear operators can be added and multiplied, but they behave differently from real numbers.

It turns out that we can come up with 25 linear operators—each one being a 4x4 array of numbers—such that when placed into the Magic Square grid, the product along any row is +1, i.e., X₁X₂X₃X₄X₅ = 1, but the product along any column is -1.  Each of these operators describes a “measurement,” i.e., a specific way of observing a quantum system to get an outcome, which is either +1 or -1.

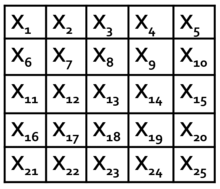
If Alice and Bob share two pairs of entangled particles and measure them with these operators to fill in their respective row or column, they will win the Magic Square game every time! (If this seems magical, that’s because it is. It’s called quantum “pseudo-telepathy,” and there’s no way to do it without entanglement.)

The curious thing here is that there is no script. If you asked Alice to tell you in advance what numbers she is going to put in the grid, she wouldn't know—those bits remain in an undetermined state until she and Bob perform measurements and find out what they are. The outcome of the strategy is inherently unpredictable, even to the players themselves.

A mathematical "proof" has thus been undone because it made assumptions that didn't hold in the physical world. This is bad news! Information science is based on assertions about what computers can and—crucially for cryptography—cannot do. The introduction of quantum physics is a game-changer that requires us to rewrite the rules.

But we shouldn’t be discouraged by this—we should use the new rules to our advantage. This is where quantum information begins.

Quantum Randomness

In 2010, I was ready to see if my dream of becoming a quantum mathematician could be realized, so I moved up to the University of Michigan computer science department. At this point, I had left behind a conventional academic track and was taking an improvised path that was sometimes exciting, sometimes quite daunting.

(Advice to young researchers: It is possible to switch fields after a Ph.D., but very difficult, so only do it if you have a good reason!)

A few months later, my colleague Yaoyun Shi found a fascinating problem for us to study. A researcher named Roger Colbeck had conjectured that multiplayer games, like the Magic Square game, can be used to create certified random numbers. Randomness is an essential resource in information science: Every time you communicate securely online, you are using a "secret key," which is a string of 0s and 1s that must be random enough that no other person can guess it.

Colbeck‘s proposal went more or less like this: Take two quantum devices that are completely untrusted, have them play Magic Square many times (with the first device in the role of Alice and the second in the role of Bob), and then check how many times they have won. Colbeck proposed proving that if the number of wins is found to be sufficiently high, the outputs can then be converted into a completely random secret key, which can then be used as a resource for communication.

This seemed like a great starting point for research: A simple question that had defied the best available techniques.

I've been asked what math research is like. My answer is like this: It's a lot of sweat, maybe a few tears, some blood (paper cuts are the worst) and a fair amount of daydreaming. (The importance of daydreaming should not be underestimated! That’s where some of the best ideas begin. Just don’t do it all the time.) Eventually, the momentum picks up, insights start to come fast, and you turn the whole thing into a successful research project.

About 2-1/2 years after Yaoyun and I happened upon it, we solved the certified randomness problem. It was undoubtedly the hardest math problem I've ever solved (so far). The proof was published last year and is available on the internet.

I’ll give two examples of insights that allowed us to carry out the proof. One was the idea of “partially trusted” quantum devices. While a “completely untrusted” device will do whatever it wants each time it is used, for a “partially trusted” device there is some fixed probability at each use that it will do what it’s supposed to do. (A clock that is untrusted might never be right, but a clock that has stopped is right at least twice a day.) We proved that completely untrusted devices can be forced to simulate partially trusted devices. This “forcing” is useful: When the device does behave properly, it gives us the random coin-flip effect exhibited by a perfect quantum superposition. Unfortunately, we don’t know when the device is behaving properly and when it’s not, but this idea of partial trust allows us to get the proof started.

Another insight that comes into play later on is the idea of a variable measure of performance for the devices. Rather than try to get a fixed number of secret bits out of the devices, we made this number change as the protocol runs. Each time the device wins the Magic Square game, we increase the number of secret bits we plan to harvest; each time it loses, we lower the number. (You could call this the philosophy of “if at first you don’t succeed, lower your expectations.” Being an optimist, I call it “if at first you do succeed, raise your expectations.”) This addresses the possibility that the performance level of the device might change over time.

We proved that Colbeck’s protocol produces perfectly secret keys—and that we can make those keys as long as we want them to be. (Longer keys mean more security.) Our results, along with those of others in the field, mean that "certified randomness" is real—and not only that, we can create it with today's technology. For those who need secure communication that they can trust, this is good news.

The Future

The game-changing effect of quantum can be used to our advantage, but it is very much a double-edged sword. In 1994, Peter Shor invented a fast quantum algorithm for factoring numbers. The hardness of factoring numbers is the basis for many existing schemes in cryptography. If this algorithm is one day implemented in a large-scale quantum computer (and, for better or worse, we're not close to having one yet), it will make many of the ways that we protect information completely insecure.

Today, I work in the Cryptographic Technologies group at NIST. Here, we create services and standards for the public to help them stay ahead of the game in the ongoing effort to protect information. We lead the Post-Quantum Cryptography project, whose goal is to design next-generation cryptography standards that are resistant to quantum computers, and also manage the NIST randomness beacon, a public randomness service. I'm also a fellow of the Joint Center for Quantum Information and Computer Science and an affiliate faculty member in the math department at the University of Maryland.

These days, large companies are competing to build quantum computers, and quantum cryptographic solutions are being made available to the public—all of which means that there are many more quantum math problems to solve.

It's an exciting time to be an applied mathematician.