Taking Measure
Just a Standard Blog

What do the following topics have in common?
- Pricing models for parking reservation systems.
- The mechanics of human walking.
- The die-down of water waves in sea ice.
- The self-hovering of unmanned aerial vehicles right above the ground.
- Bright cosmic infrared arcs that form when stellar dust meets the solar wind.
- The reconnection of whirlpool-like vortices in exotic “superfluids,” which flow without friction.
They are all subjects of technical papers published in 2019 that cite a remarkable 1914 paper published by a physicist at the agency that became the National Institute of Standards and Technology (NIST). Indeed, the Web of Science academic database records that paper as the most-cited paper of all that were published in the year 1914: a part of a fervent scientific decade in which Nobel laureates such as Marie Curie, Albert Einstein, Ernest Rutherford, Niels Bohr, J.J. Thomson, and William Lawrence Bragg were active.
Edgar Buckingham, a physicist at the National Bureau of Standards (NBS), was the author of that paper. In it, he laid out what has become known as the "Buckingham pi theorem," which provides a framework for a problem-solving approach called dimensional analysis.
Isaac Newton knew about dimensional analysis and used it in his masterpiece, the Principia Mathematica. Science students learn about the procedure by their first year of college. NIST researchers use it every day, for it provides a universal structure for solving problems of science and engineering and the design of experiments.
The basic idea of dimensional analysis is to consider all possible products and ratios of the physical dimensions of the variables in the system under study. Important physical dimensions in many applications involve mass, length and time.
A simple example is the determination of the area, A, enclosed by a circle of radius, r.
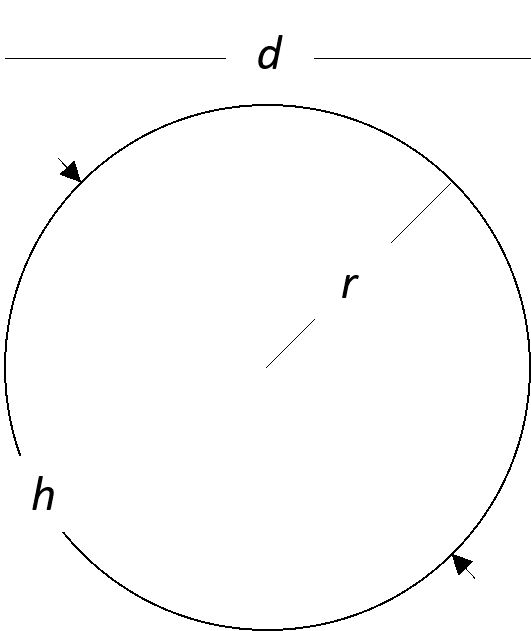
There are many choices for describing the size of a circle, such as its radius, r, its diameter, d, or half of its circumference, h. But all of these are proportional to each other — they each have the physical dimensions of length — and quantities such as d/r and h/r are just numbers — without any units or dimensions. There is only one independent physical dimension of length, which we can take to describe by r, measured in meters. The area, A, has dimensions of square meters = meters2 = meters x meters, and so dimensional analysis requires that A(r) = 𝜋 x r2, where 𝜋 is a pure number that today we call “pi” (get it — March 14??). This expression is the only way to generate a result in square meters once we have decided on the standard of length, r.
One more bit of background that will help you follow the rest of the argument:
A(r)= 𝜋 x r2 is something in mathematics called a function. A function, f, is like a machine that takes an input value, x, and produces a unique output value, f(x). Newbies are usually surprised at how much one can milk this very simple idea — see the NIST Digital Library of Mathematical Functions for examples. In this case, A(r) takes the input, r, in units of meters, and outputs the value A(r) = 𝜋 x r2, in units of meters2.
What if we have multiple independent standards of length in our system? That’s the issue addressed by Buckingham. For example, what is the area of the ellipse inscribed within this rectangle?

We have two independent lengths that describe the rectangle, a and b. Thus, we could choose to write A = a x b x f(a/b), where f(a/b) is some function of the dimensionless ratio a/b, which describes the shape rather than the size of the ellipse. This expression captures the evident fact that if a and b are increased by a common factor of L, the shape of the ellipse stays the same and its area increases by a factor of L2. In honor of this day, I note that in fact f(a/b) = 𝜋 for any value of a/b.
In his 1914 paper, Buckingham uses a college-level branch of mathematics known as linear algebra to provide a systematic framework within which such dimensional scaling factors can be determined. Here is an example he gives of its application: to find the thrust of a ship’s propeller that is required to maintain the ship’s speed.
The thrust depends upon six independent dimensional variables: the diameter and rotation rate of the propeller, the ship's speed, the acceleration of gravity, and the density and viscosity of seawater. How does one even begin to solve such a problem? Buckingham shows that there is a unique set of combinations of the parameters mentioned above that “tells us without any experimentation at all” what the essential relationships must be.
A testament to the power of this approach is its continued use a century hence, across a wide range of subjects indicated by the examples shown at the beginning of this essay. Those are but a sample of the 131 papers published in 2019 that cite Buckingham's original paper, according to the Web of Science. More than 1,400 citations have been made so far, and at an increasing rate — something quite unusual for a century-old paper.
Buckingham's achievement derived from a keen understanding of the process of physical measurement, and it put working clothes on Lord Kelvin's dictum: "When you can measure what you are speaking about, and express it in numbers, you know something about it." It is a distinctive contribution to science, and likely one of the most influential.
About the author
Related Posts
Comments
Charles(aka Bruce and/or Carbon Tungsten Chlorine Argon Potassium), you continue to amaze me and the rest of the world with your mastery of interesting obscurities.
If I have not seen as far as others, it is because giants were standing on my shoulders!
I love numbers
Good article, thanks. It would be nice to read the paper without paying $35.
The American Physical Society will give free access to any Physical Review article to anyone who applies via a U.S. public or high school library. For details, see https://journals.aps.org/free-access-for-us-public-and-high-school-libr…
I should also note that the full texts of many classic physics papers can be found via Google Scholar, ResearchGate and other such tools that are widely used in the physical sciences research community.
I have always wanted to see the Dimensional Analysis of robot payload motions in terms of inertia and material density. When the CanadaArm 2 on the NASA ISS transports a suited astronaut with their tools to an EVA worksite -- like the site of a battery changeout -- the CanadaArm astronaut operator moves the payload very slowly. It would be very useful to perform the Dimensional Analysis (DA) of the 'envelope' or recommended limits for the elemental motions of all the involved robot joint gearmotors. Is the author aware of any such 'inertia' and 'materialdensity' DA of robot payload motion.
I don't know of work on this subject, but I am certainly no expert. You might have a look at https://ntrs.nasa.gov/search.jsp?R=19740008732 It uses the approprite language, and Google Scholar indicates that 625 subsequent publications have cited it.
Charles, my hat is off to you. Your ability to explain scientific concepts to a general audience, without dumbing it down, is admirable. And I really appreciate the reference to the DLMF!jBQzo,
Many thanks Dan!
You state that "Those are but a sample of the 131 papers published in 2019 that cite Buckingham's original paper, according to the Web of Science. More than 1,400 citations have been made so far, and at an increasing rate". This implies that nearly 10% of the citations over the past century were made in 2019. Surely that cannot be so. The truth is...…..






Wonderfull