Everyday Time and Atomic Time: Part 4

This is part 4 in a series. Read part 1, part 2 and part 3. 

Greenwich Mean Time

In the previous essay I introduced mean solar time, which averaged the annual variation in apparent solar time so as to generate a time scale that was more consistent with the time scale generated by clocks that used a mechanical device to realize the reference frequency. The device that generated the reference frequency might produce an event every second, but other configurations were possible. In every case, the device that generated the reference frequency was coupled to a second system that converted the reference frequency to a series of one-second ticks that were used to drive the clock display. The source of the reference frequency and the counting system were designed together to generate the one-second ticks.

In 1884, the International Meridian Conference defined the meridian passing through the Royal Greenwich Observatory in Greenwich, England, as 0 degrees longitude, and other meridians were specified in degrees east or west of this origin. Greenwich Mean Time (GMT) is then defined as mean solar time as observed at the Greenwich meridian.

It is important to emphasize that Greenwich Mean Time is an example of mean solar time. It is a time scale derived from astronomy. This is important because the term GMT is often used to designate time scales derived from atomic clocks, and this usage is technically not correct. I will return to this point later.

When Does the Day Begin?

Civilian time defined the start of the day at midnight, but the astronomical community usually defined the start of the day as noon. There were several reasons for this choice. In the first place, if the date changed at noon, then the date would not change at night when astronomical observations were made. In the second place, solar time is the angle between the position of the Sun and the local meridian, and this angle goes through zero at noon, so it was reasonable to define the start of the day to coincide with the value of the angular position of the Sun with respect to the meridian. Finally, there is an obvious, readily observable astronomical event at noon, but there is no corresponding event at midnight.

Adopting the astronomical definition for the start of the day at noon in civilian time was out of the question — a change in the date in the middle of the working day would lead to no end of confusion. Instead, the astronomical community adopted the civilian definition on 1 January 1925. The instant 31 December 1924 12:00:00 GMT in astronomical time (equivalent to midnight between 31 December 1924 and 1 January 1925 in civilian time) became 1 January 1925 00:00:00 GMT for astronomical purposes (thus agreeing with the civilian definition), and the subsequent days started at midnight for both astronomical and civilian purposes. The old definition was renamed Greenwich Mean Astronomical Time (GMAT). The day starts at midnight in all modern time scales, and this instant is assigned the time 00:00:00 of the new day, although the name 24:00:00 with respect to the previous day is also used. The name of the previous second is 23:59:59.

Simplified Celestial Navigation

A navigator on a ship at sea could determine the latitude of the ship by observing the angle between the Sun and the horizon at apparent solar noon and combining this measurement with a table giving the angular position of the Sun with respect to the equator for each day of the year. In the Northern Hemisphere, the angle between the horizon and the star Polaris (the North Star) could also be used. The determination of the longitude of the ship was more difficult.

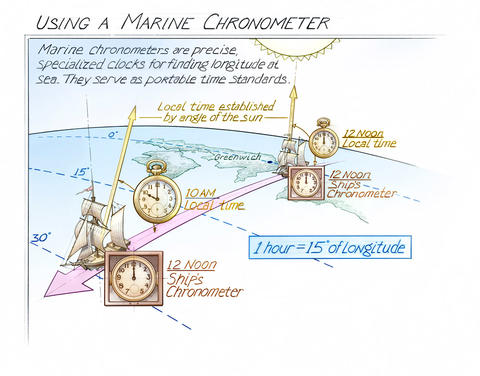
The determination of longitude depended on having a source of GMT on the ship. For example, suppose that the navigator observed that apparent solar noon at the location of the ship occurred at 12:57:00 p.m. GMT as measured by the clock on the ship. The navigator would then convert apparent solar time to Greenwich Mean Time by using the value given by the equation of time for that date. Suppose that applying this correction gave a time of 1:00:00 p.m. GMT. Since Earth rotates at a rate of 360 degrees/24 hours = 15 degrees/hour, the navigator would determine that the ship was located 15 degrees west of Greenwich, since noon in Greenwich Mean Time at the location of the ship occurred one hour later than noon at Greenwich.

There were several methods for the navigator on a ship to determine GMT. The straightforward method was to use a marine chronometer — a precision clock that was set to GMT and had sufficient accuracy to maintain this time scale for the duration of the voyage (often months). The first practical chronometers were developed by John Harrison in about 1750 and by others in other countries at about the same time.

Various astronomical methods were proposed before chronometers were available. Galileo proposed a method based on observing the eclipses of the moons of Jupiter and comparing the observed eclipses with published tables.

The method of lunar distances was another way of determining GMT at sea. The “lunar distance” is the angle between the apparent position of the Moon and the apparent position of a specific star. This measurement is combined with a nautical almanac, which includes a table of these distances for every day of the year. The apparent position of the Moon moves only about one-half degree per hour (360 degrees in about 27.5 days — the period of the orbit of the Moon with respect to the distant, fixed stars). The apparent size of the Moon as observed on Earth is also about 0.5 degrees, so the apparent motion of the Moon is about one moon-diameter per hour. It was not easy to measure the position with adequate accuracy on a moving ship.

The orbital period of the Moon is longer for an observer on Earth. In the “new moon” configuration, the Moon is in the same direction as the Sun from the perspective of an observer on Earth. The orbit of the Moon is inclined with respect to the plane of the orbit of Earth, so that this configuration normally does not result in an eclipse of the Sun. When the moon returns to this same orientation with respect to the distant fixed stars, Earth has moved along its orbital path, and the line between Earth and the Sun has changed by about 360 × (27.5/365) degrees. The Moon must continue in its orbit by this amount until it returns to the “new moon” configuration. The speed of the Moon in its orbit is approximately 360/27.5 degrees per day, so that time for the moon to rotate through this angle is the ratio of these two quantities or about 27.52/365 = 2.04 days. The orbital period of the Moon from the perspective of Earth is thus about 27.5 + 2.04 = 29.54 days.

A Simple Example of Celestial “Navigation”

In the figure, I am standing on the meridian line that passes through Old Town Square in Prague, Czech Republic. The meridian line is at 14° 25’ 17’’ east longitude, so that noon in mean solar time occurs on this meridian about 58 minutes before noon GMT or at 11:02 a.m. GMT. The picture was taken at 11:02 a.m. GMT, and the very small offset of my shadow from the meridian line is the effect of the equation of time — the difference between apparent solar time and mean solar time on that day.

The latitude of my location could be determined by using the ratio of my height to the length of my shadow at local noon (when my shadow is directly along the meridian line) and combining this value with the latitude of the Sun on that day.