Cybersecurity Insights
a NIST blog
Privacy-Enhancing Cryptography to Complement Differential Privacy

In previous posts we discussed many aspects of differential privacy: what it is, what it is useful for, and how it is applied to data analysis problems. All of those ideas can be applied once you get your hands on a whole dataset. What if the data you are interested in extracting insights from belongs to mutually distrusting organizations? For example, say you run a pumpkin spice latte stand and are wondering if your pumpkin spice supplier is overcharging you compared to the industry-wide average. You are willing to participate in a study that computes this average, but not comfortable giving your raw expense data directly to a third party. Remarkably, computing this average without sharing any raw data is possible using advanced cryptographic techniques, and these techniques can be used together with differential privacy to enable data sharing while also protecting privacy. To help us understand how those techniques work, we are delighted to introduce Luís Brandão and René Peralta, who are with the Privacy Enhancing Cryptography (PEC) project at NIST.
DISCLAIMER: Opinions expressed here are by the authors and should not to be construed as official NIST views. Brandão is at NIST as a Foreign Guest Researcher, Contractor from Strativia. Any mention of commercial products or reference to commercial organizations is for information only; it does not imply recommendation or endorsement by NIST, nor does it imply that the products/organizations mentioned are necessarily the best available for the purpose.
In this post, we illustrate how various techniques from privacy-enhancing cryptography, coupled with differential privacy, are useful to protect data privacy while enabling data utility. Of notable interest is the setting where there are multiple sources of relevant data, each having privacy constraints about data sharing. Privacy-enhancing cryptography is naturally suited to resolve challenges in multi-party and interactive scenarios, avoiding the sharing of data across parties. Its combined use with differential privacy broadens the set of problems that can be handled in a privacy protecting manner. In this post, we consider a use case related to private medical data, but the ideas can easily transfer to myriad other settings.
Protecting data privacy across multiple datasets
Alice is the data steward at hospital HA, responsible for a database of patient medical records. Similarly, Bob is the data steward at another hospital HB. Alice and Bob learn of Rya’s ongoing research about correlations between patients’ age and diagnosis. Alice and Bob would like to help Rya, since the research could provide useful insights to derive better medical practices. However, there are privacy restrictions that prevent Alice and Bob from sharing their databases.
Suppose Rya is interested in learning the number of patients diagnosed with a condition X, by age-range. Differential privacy allows Rya to obtain an approximate result from each of the two hospitals, each tweaked by a noise addition in order to protect privacy. However, the restriction to two separate results has shortcomings: (1) when combining the two results, Rya is unable to make corrections that may be required because of possible duplicate entries; (2) the pair of individual replies leaks information about hospital differences, which is unrelated to Rya’s goal.
In contrast to the above scenario, privacy-enhancing cryptography (PEC) enables Rya to interact with Alice and Bob to obtain a combined response that is corrected with respect to duplicate entries. This is done without Alice and Bob sharing data between themselves, and without Rya learning anything beyond the intended output. PEC can be combined with differential privacy techniques to provide the best tradeoff between privacy and accuracy. Table 1 illustrates how errors may be introduced when not using PEC. The error is in the sum of two correlated counts, which overestimates the true count in the union of two sets. These errors (with rates above 25 % in the example) can significantly hinder the utility of the results.
Table 1: Measure (N) of the number of patients with diagnosis X
|
Age range |
Without differential privacy |
With differential privacy |
||||||||
|
Exact counts |
Error rate r |
Differentially private counts |
Error rate r |
|||||||
|
A |
B |
∪AB |
If N=A+B (no PEC) |
If N=∪AB (with PEC) |
A |
B |
∪AB’ |
If N=A’+B’ (no PEC) |
If N=∪AB’ (with PEC) |
|
|
0–30 |
8 |
11 |
15 |
26.7 % |
0 % |
9.2 |
10.1 |
16.5 |
28.7 % |
10 % |
|
31–60 |
123 |
85 |
172 |
20.9 % |
0 % |
119.5 |
87.2 |
168.3 |
20.2 % |
2.2 % |
|
61–120 |
428 |
632 |
660 |
60.9 % |
0 % |
433.7 |
633.1 |
656.8 |
61.6 % |
0.5 % |
Legend: A (counts at hospital HA); B (counts at hospital HB); ∪AB (counts at the union of hospitals HA and HB); A’, B’, ∪AB’ (differentially private versions of A, B, ∪AB); r = N/∪AB − 1.
What is safe to compute? As discussed in previous posts, differential privacy techniques add noise to the exact result of a query, to limit privacy loss while still enabling a useful answer to relevant queries to a database. From a privacy perspective, the approximate result is “safer” than an accurate answer. PEC techniques achieve something different: they circumscribe the disclosure to only the specified final output, even if the source inputs are distributed across various parties. Such disclosure is “safer” (with respect to privacy and accuracy) than replies that would include isolated answers from each separate source. This is achieved with cryptographic techniques that emulate an interaction that would be mediated by a (non-existing) trusted third party. The PEC and the differential privacy paradigms can be composed to enable better privacy protection, namely in scenarios where sensitive data should remain confidential in each individual original source. Differential privacy adjusts the query result into a noisy approximation of the accurate answer, which PEC can compute without exfiltrating additional information to any party.
Privacy-enhancing cryptography techniques
The next paragraphs consider five privacy-enhancing cryptography techniques: secure multiparty computation (SMPC), private set intersection (PSI), private information retrieval (PIR), zero-knowledge proofs (ZKP), and fully-homomorphic encryption (FHE). We illustrate how they can apply, in composition with differential privacy, to Rya’s research setting. The examples include settings that have to handle more than one database, account for privacy restrictions from Rya, and ensure correctness even if some parties misbehave.
SMPC. With secure multiparty computation (SMPC) (e.g., Yao and GMW protocols), Rya can learn a statistic computed over the combined databases of Alice and Bob, without actually combining the databases. Alice and Bob do not see each other’s data, and Rya learns nothing about the databases, other than what can be inferred from the (differentially private) obtained statistic (see Figure 1).
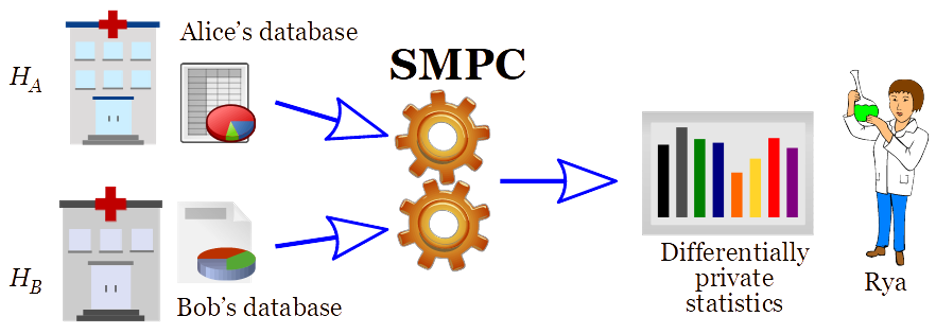
The application of SMPC together with differential privacy, as showcased in Figure 1, constitutes a more secure alternative to “central DP” and to “local DP”, where a curator combines the data but also becomes subject to privacy breaches, as explained in a previous post. Central DP compromises on security, by requiring a potentially hackable curator to serve as custodian of the data from multiple hospitals, to be able to answer queries in a DP manner. Local DP makes a tradeoff between privacy and accuracy, mitigating the foreseeable case of the hacking of the curator, by requiring that the data sent from each hospital to the curator has been DP-protected. SMPC (of differentially private statistics) enables the best of both worlds: it provides the best-possible accuracy (as in central DP), and it avoids the leakage potential from the possible breach of a curator (in both central and local DP).
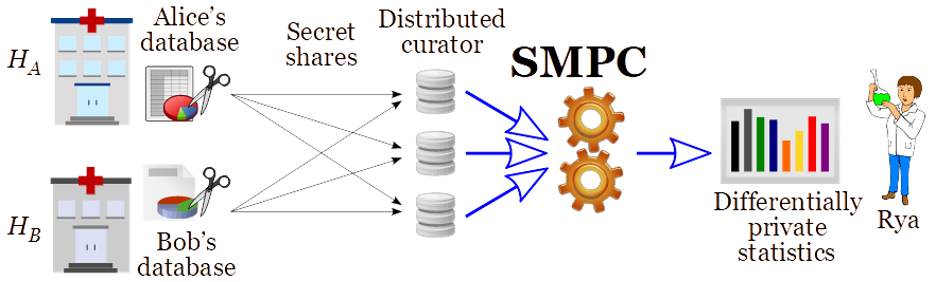
A different application of SMPC, to avoid requiring online availability of the original sources (the hospitals), is to use a distributed curator (see Figure 2). Here, the data from each hospital is secret shared, so that no sole component of the curator knows the data, but a threshold number of them is sufficient to answer any query, i.e., using SMPC to compute over the secret-shared data. Presently, the MPC Alliance is a consortium that joins more than 40 companies interested and actively engaged in developing and implementing SMPC solutions.
PSI. With private set intersection (PSI) (e.g., Matchmaking and Oblivious Switching protocols), Alice and Bob can determine the set of patients that are common across their databases, without sharing any information about other patients. Naturally, this intersection can be considered sensitive information that should remain private. A variant called PSI cardinality can be used to compute statistics about the common patients, such as how many there are, without divulging the set itself (see Figure 3). The mentioned PSI# can also be considered per age and per diagnosis.

We note that even the cardinality of the intersection may be sensitive information. Therefore, this multi-party statistic can itself be subject to differential privacy protection. From a different angle, the statistic can also be useful for the hospitals to determine how to parametrize their differential privacy protection level for subsequent queries from external researchers. This may improve privacy and/or accuracy in settings where Rya will later be separately querying both hospitals. Conceivably, this could be useful in a setting related to the COVID-19 pandemic, as considered in an application where a party learns a risk of infection based on the number of encountered persons that have been diagnosed as infected.
PIR. With private information retrieval (PIR), Rya is allowed to learn the result of a query sent to Alice’s database, without Alice learning what was queried (see Figure 4). Recalling our example from Table 1, Rya can learn the differentially private approximation (A’=119.5) of the number (A=123) of patients in HA, with diagnosis X and within the age range 31–60, without Alice learning the queried age-range. Naturally, this can be generalized to hide which diagnosis (X) was queried.

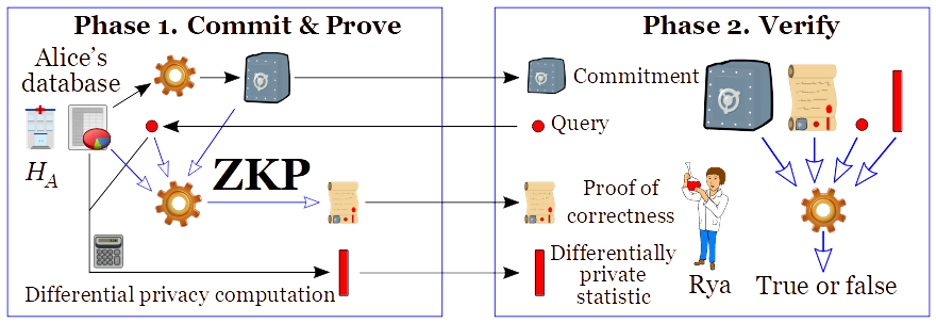
ZKP. Zero-knowledge proofs (ZKPs) allow making proofs about data that has somehow been “committed” (for example, by disclosing an encrypted version of a database), without revealing the actual data. Thus, once the data has been committed, a database owner can prove that the reply given to a certain query correctly relates to data that has not changed. This is a great tool for allowing accountability while protecting privacy. In particular, ZKPs can also be used to enable other PEC techniques (such as SMPC, PSI and PIR) in the so-called malicious model, where any of the parties (Alice and Bob) could otherwise undetectably deviate from the agreed protocol. For example, a ZKP can be used by Alice to prove to Rya that an answer satisfies an appropriate differential privacy protection, i.e., resulting from a correct noise addition, with respect to the original secret database (see Figure 5). Presently, zkproof.org is an open initiative that seeks to mainstream the development of interoperable, secure, and practical ZKP technology.
FHE. Fully-homomorphic encryption (FHE) allows computing over encrypted data, without knowing the secret key. In other words, someone without the secret key (needed to decrypt) is able to transform a ciphertext (i.e., the encryption of a plaintext) into a new ciphertext that encrypts an intended transformation of the plaintext. Conceptually, Rya can encrypt the intended query, send it to one or various hospitals, and then let the hospitals transform the encrypted query into an encrypted DP-protected reply, which Rya can later decrypt (see Figure 6). The computation can be made sequentially across hospitals, with each new transformation remaining encrypted until the final stage of decryption by Rya.
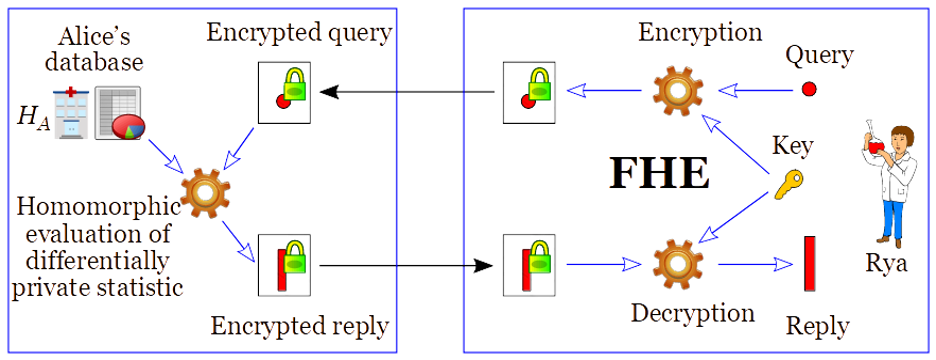
FHE is a natural primitive to enable privacy-preserving delegation of computation. The reader may note that the FHE use-case in Figure 6 is very similar to the PIR use-case in Figure 4. Indeed, FHE can be used as a primitive for a number of other privacy-enhancing cryptography tools, including PIR, PSI, and SMPC. A typical implementation benefit is that it enables solutions with minimal communication complexity. A possible downside of FHE is that it can be computationally more expensive than other solutions. However, there are applications for which FHE is practical, and the field is rapidly improving. The homomorphicencryption.org initiative is promoting the standardization of FHE.
Conclusion
The roles of privacy-enhancing cryptography (PEC) and differential privacy are significantly different, but they are complementary. Both types of techniques are applicable to protect privacy while enabling the computation of useful statistics. In conclusion, the toolkit of the privacy-and-security practitioners should include PEC tools. They provide additional utility while protecting privacy, including in interactive and multi-party settings that are not amenable to be handled by standalone differential privacy. For more PEC details and examples, follow the NIST-PEC project. This is an exciting area of development.
Coming Up Next
In this post we discussed techniques for linking sensitive data across multiple data owners. But how do we know if the differentially private results we get out will be useful? To answer this question requires applying the right utility metrics, which is the topic of our next post. Stay tuned!
This post is part of a series on differential privacy. Learn more and browse all the posts published to date on the differential privacy blog series page in NIST’s Privacy Engineering Collaboration Space.



