What Is Quantum Cryptography?
The rules of quantum physics could someday safeguard your data.
What is cryptography?
For centuries, royal figures, government officials and military officers — along with spies and assassins — have used secret codes to protect their confidential messages. These individuals were performing early versions of cryptography — employing mathematical techniques to protect the security of information.
These secret codes, known as ciphers, could be as simple as taking a message and shifting each letter of the alphabet by a certain number of positions so that A became D, B became E, etc. But cryptography has evolved greatly since these earliest examples.
Nowadays, digital devices such as computers routinely carry out mathematical operations to scramble information in highly complex ways. In addition to being much more technologically advanced, modern cryptography frequently includes authentication — verifying that both the sender and the receiver of information really are who they say they are.
What is quantum cryptography?
Quantum cryptography is a set of methods that uses the quirky — but well-understood — rules of quantum mechanics to securely encrypt, transmit and decode information. Quantum cryptography employs quantum devices, such as sensors capable of recording individual particles of light (photons), to protect data from an adversarial attack. Although technically challenging, quantum cryptography promises advantages over classical, nonquantum cryptographic systems. For instance, the quantum approach has the potential to better detect and thwart eavesdroppers who try to intercept data.
One early example of a quantum cryptographic protocol, known as quantum key distribution (QKD), uses a string of computer bits or characters (called an encryption key) shared by two trusted partners to scramble and unscramble data. Although the encryption key itself is not quantum, it is transmitted using quantum particles — photons. In 2004, Austrian scientists employed QKD to establish a secure connection for the transfer of funds from a bank to Vienna City Hall.
QKD systems, however, still have technological and theoretical loopholes, some of which could make it possible for eavesdroppers to intercept and decode messages. Because of these current limitations, the National Security Agency does not recommend using QKD for national security systems.
How can quantum physics protect information?
The primary principles of quantum mechanics that help safeguard data are superposition and entanglement.
In superposition, objects in the quantum world, such as atoms, electrons and photons (particles of light), can be in two or more energy states at the same time.
In the famous hypothetical example of Schrodinger’s cat, a feline in a box can be simultaneously dead and alive, but once the box is opened and someone observes it, the cat is either dead or alive.
For a real-world example of superposition, imagine a photon passing through a piece of polarizing film, such as those used in sunglasses. The film is a special material etched with a series of parallel lines. If you arrange the film so that the lines are vertical, the photon will pass through if its electric field vibrates vertically; this is known as vertical polarization. The photon will be blocked if its electric field vibrates horizontally (horizontal polarization).
But before the photon strikes the film, the photon can be in a superposition of horizontal and vertical polarizations, as if it’s simultaneously polarized in both directions. Once the photon strikes the polarizing film, the superposition “collapses” so that the photon now has a definite polarization, either vertical or horizontal.

Researchers can use this phenomenon of superposition to encode information. A horizontally polarized photon can represent a 0, and a vertically polarized photon can represent a 1. This is known as a quantum bit, or qubit.
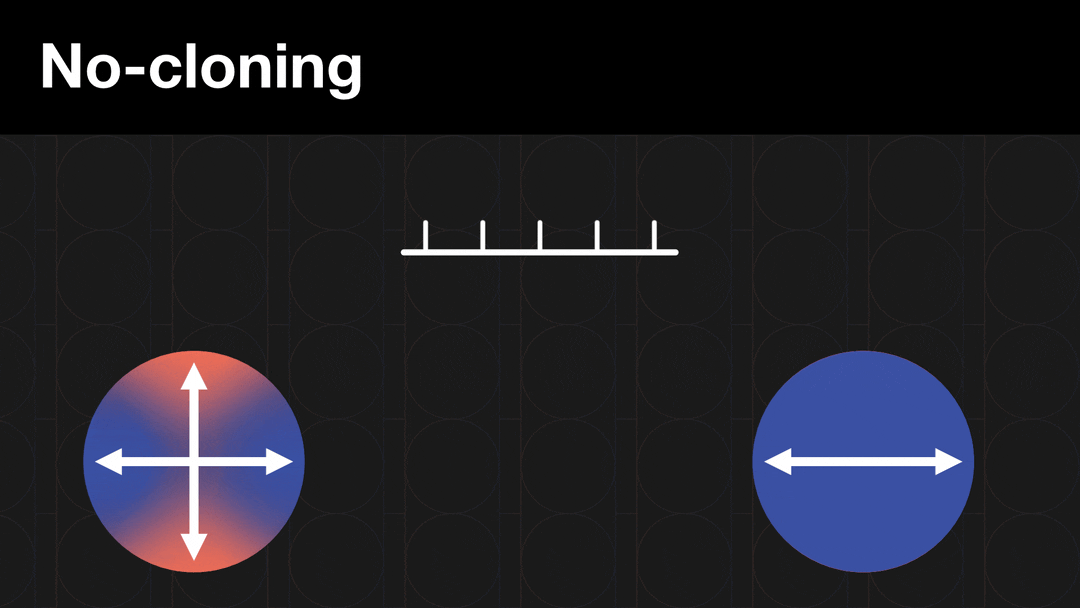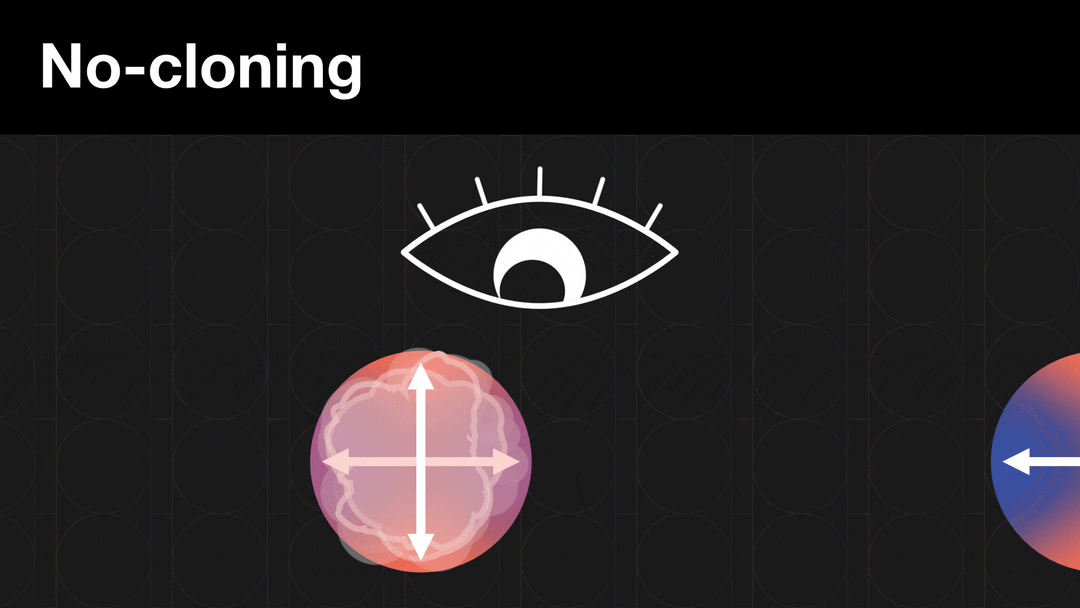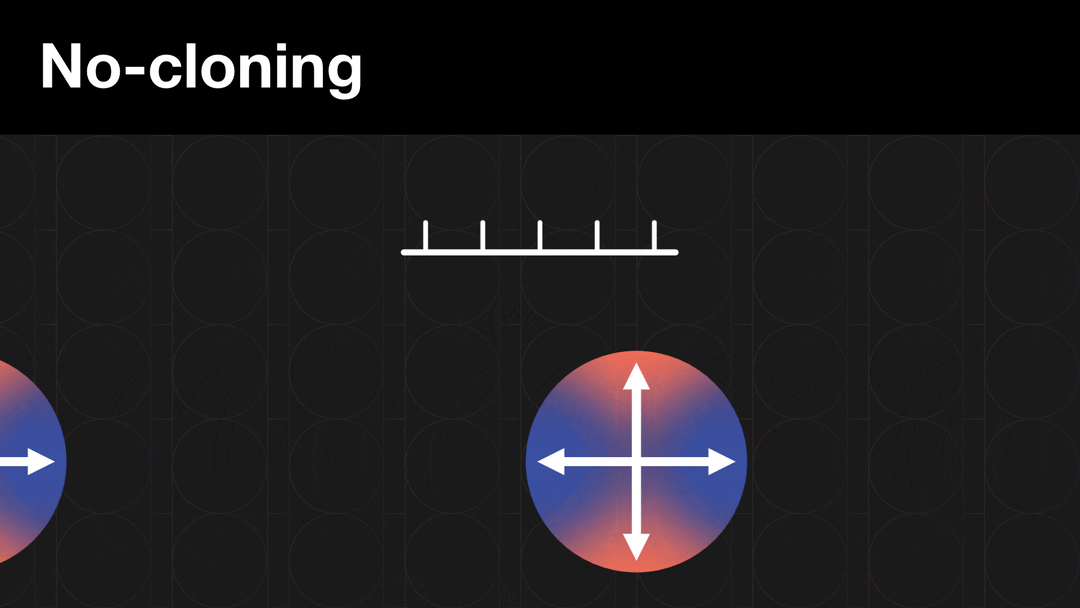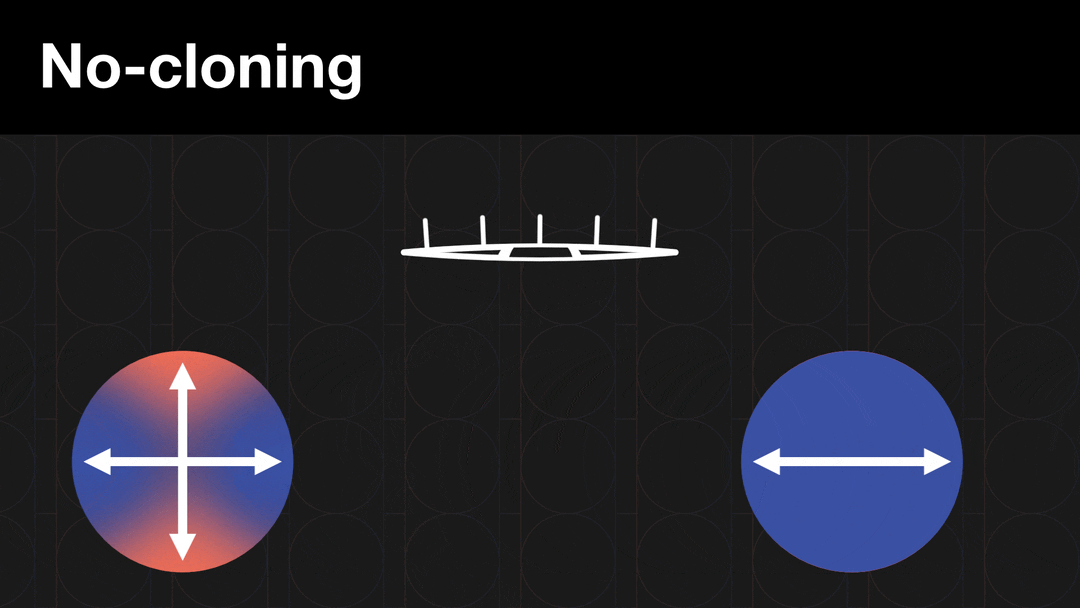
Qubits can be in superpositions of 0 and 1 — which can be very useful for processing data — but they are fragile. You can’t measure them without destroying their superposition and forcing them to become either a 0 or a 1.
Destructive as it sounds, the collapse of a superposition has a silver lining. Measuring a qubit makes it impossible, in theory, to steal and copy the information encoded by these states.
This “no-cloning rule” means that anyone trying to intercept or copy a code based on one or more qubits will destroy the code instead of deciphering the message, alerting the sender and receiver that their message has been hacked. In contrast, adversaries can copy traditional “classical” bits perfectly without being detected.
The quantum principle of entanglement takes superposition to the next level. In quantum entanglement, two (or more) particles can be linked in such a way that if you measure the property of one particle you automatically determine the property of the other — even if they reside on opposite sides of the globe. At first glance, that might not seem so unusual. For instance, if you have two gloves — one black and one white — in a box and pull out a white glove, of course the remaining glove is black.
But the quantum realm isn’t so decisive. Instead of having one black glove and one white glove, each glove is in a superposition of black and white until it is examined. When one of the gloves is observed, it assumes a definite color — black, for instance. That observation “forces” the other glove, even if lies far away, to take on the opposite color, white.
What are some of the challenges in employing quantum cryptography to securely transmit and receive data?
Quantum cryptography requires extraordinarily sensitive, low-noise devices. Such devices could reliably send and record individual photons, atoms or other particles to encode and transmit a message.
But no instrument works perfectly. The physical limitations of the equipment create potential flaws in quantum cryptography. An eavesdropper can exploit these imperfections to evade detection.
For example, many quantum encryption systems encode information using photons. It’s virtually impossible to produce a detector that registers every photon that hits it or to deploy light sources that always produce one photon at a time; occasionally they release multiple photons simultaneously.
False detections (such as recording a photon when one isn’t there) must be kept to a bare minimum. The full set of photons in a message must be sent and received to correctly encrypt and decipher the message. And the hardware must be built to resist tampering by an interloper trying to steal the message.
In theory, scientists can close many of these loopholes by using more sophisticated protocols. These protocols are sometimes called “device-independent,” because their security is in some sense “independent” of many physical properties of the devices that carry out the protocol.
Building such devices isn’t easy, but NIST is at the forefront of developing and building sensitive detectors, an important building block, with applications far beyond quantum cryptography. These include single-photon detectors that operate at temperatures near absolute zero, which minimizes noise and enables individual photons to be recorded with high accuracy.
How would a real-world quantum communications system transmit information?
A real-life quantum communications system may use photons to carry information over hundreds of kilometers inside an optical fiber. Over such large distances, photon absorption in the fiber limits the ability to convey information and to preserve the fragile quantum properties of photons, such as entanglement. Those properties are essential to making quantum cryptography work.
To circumvent the problem, NIST scientists and other researchers are experimenting with using photons in a series of shorter optical fibers that are linked together in a quantum network. Absorption can be a problem even in a network of shorter fibers. In a classical (nonquantum) system, that loss can be overcome by copying and amplifying the information, but the no-cloning theorem forbids that from happening in a quantum system. Instead, scientists are developing devices called quantum repeaters, which will distribute and swap entanglement among the photons in a quantum network, generating a single long-distance entanglement from many short-distance entanglements. This allows for the transmission of quantum information over much greater distances than would otherwise be possible.
How could quantum cryptography authenticate that the sender of a message is who they say they are?
Quantum cryptographic systems aim to provide a secure communications channel between senders and recipients. But how can you be sure that the sender or receiver isn’t an impostor?
One way to check is to verify their location. For instance, if a diplomat is sending a confidential message back to her home country, she’d like to verify that the computer server she’s communicating with is actually in her country.
To do so, researchers are developing a technique called quantum position verification (QPV), in which recipients would be required to manipulate qubits in a particular way that can only be performed if they’re located at the position they’re supposed to be.
QPV has not yet been deployed. Scientists at the Joint Center for Quantum Information and Computer Science, a research partnership between NIST and the University of Maryland, are among those studying how to make QPV work in the real world.
Even at its best, QPV can only verify where the sender is, not who they are. To authenticate a sender, a verifier would combine a quantum cryptographic method with a digital certificate — an electronic file that acts as a form of online identification. The certificate contains such information as a user’s name, company or department, and the device’s Internet Protocol (IP) address or serial number. Digital certificates contain a copy of a public key from the certificate holder, which must be matched to a corresponding private key to verify that it is real.
What is quantum randomness, and how can it play a role in quantum cryptography?
Random numbers are vital to encrypting and securing data in electronic networks, an operation that occurs hundreds of billions of times a day. But these numbers are not certifiably random in an absolute sense. That’s because they are often generated by classical (nonquantum) physical devices whose supposedly random output could be generated by components (such as computer chips) that have predictable behavior.
For instance, a coin flip may seem random, but its outcome could be predicted if one could see the exact path of the coin as it tumbles. A computer random number generator may rely on software that generates a sequence of bits from a starting point known as a “seed.” The seed, however, is not completely random and can exhibit predictable patterns.
Quantum randomness, on the other hand, is fully random.
A true random number generator can only be based on a quantum system, because only quantum particles act in completely unpredictable ways. One example is the radioactive decay of an atom, whose behavior is governed by quantum mechanics. The precise time at which radioactive atoms decay is completely random, and this random behavior could be used to generate random numbers.
For example, if you are watching atoms decay with a watch that starts at zero seconds, those that decay during “odd” seconds (1, 3, 5, etc.) can be assigned as 0 and those that decay during “even” seconds (2, 4, 6, etc.) can be assigned as 1. In that way, a radioactive sample of atoms could generate a random string of 0s and 1s.
By taking advantage of the similarly unpredictable behavior of photons moving through a maze of lenses and other optical components, researchers at NIST have developed truly random number generators.
Researchers rely on quantum randomness to securely transmit information. The random numbers form a secret “key” to encode and decode the data. Although encoders often employ mathematical algorithms that can approximate a string of random numbers, such a key could still be vulnerable to hackers because it is not entirely unpredictable.
The quantum-based method generates digital bits (1s and 0s) using photons and is part of an ongoing effort to enhance NIST’s public randomness beacon, which broadcasts random bits for applications such as secure computation involving computers at multiple locations on a network.
How can quantum cryptography secure the processing of our private data on remote computer networks?
Scientists are working to use quantum cryptography to ensure the security of our data beyond simple communication. Businesses and other organizations often send our personal data to remote computer systems, or the cloud, accessed across the internet because they lack the computing power to process the data themselves. However, that poses a problem.
Although the information is encrypted before it reaches these systems, it must typically be decrypted for networks to process it. That leaves the data vulnerable to potential hackers — including someone operating the network who may not be trustworthy.
Using the quantum principles of superposition and entanglement, researchers have figured out a way to help close this particular loophole. Data that is encrypted using qubits can be sent to a network in such a way that it can be processed and securely returned without the remote network ever knowing the nature of that information or what computation problem the network was asked to perform. This strategy of keeping information safe is known as blind quantum computing.
In summary, quantum cryptography harnesses the fundamental laws of quantum mechanics to protect data and authenticate the sender and receiver of that data. NIST scientists are working to test and perfect quantum cryptographic systems, build sensors that can accurately transmit and receive quantum-encrypted messages, and set standards for the capabilities of quantum cryptographic systems.
Here’s a quantum twist for you: The same principles underlying quantum cryptography have made it possible to develop quantum computers, which have the potential to break many nonquantum forms of encryption, including those currently safeguarding data on the internet. That’s where post-quantum cryptography comes in. Post-quantum cryptography prepares for that future era by updating existing classical (nonquantum) computers with algorithms resistant to code-breaking by quantum computers. Learn more about post-quantum cryptography.

