Uncertainty Quantification in Computational Materials Science

Summary

We are investigating and promoting applications of uncertainty quantification to problems in computational material science. Detailed investigation of promising use cases will lead to creation of guidance and best practices in the use of numerical simulation to inform decision making in the materials development cycle.

Description

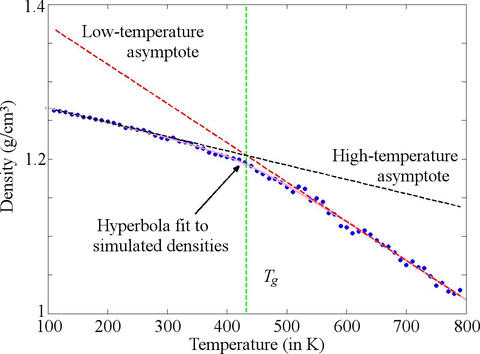
Molecular dynamics simulation of density of an aerospace polymer as a function of temperature.

Industry and other stakeholders increasingly rely upon simulations to inform their decisions. To make this strategy routine and reliable these simulation results must be accompanied by quantitative statements of their quality.  Uncertainty quantification refers to the growing suite of tools situated at the crossroads of statistics, mathematics, numerical analysis, and computational physics that are designed to accomplish this task.

Major Accomplishments

Our work aims to develop technical tools for uncertainty quantification as well as build a larger community of practice within computational materials science. Representative examples are:

Uncertainty Quantification in Molecular Dynamics Simulations

We are developing applications of uncertainty quantification to molecular dynamics simulations of polymer systems of interest to the aerospace industry.  This project is currently researching tools to assess the uncertainty of computationally derived measurements of the glass-transition temperature, yield-strain, and radial distribution functions for molecular systems.

Uncertainty Quantification for Finite Element Simulations

The finite element method is a simulation workhorse used throughout industry to solve problems in computational fluid mechanics, structural analysis, electromagnetics, and acoustics to name only a few. We are developing uncertainty quantification analysis techniques based on design of experiments to assess quantitative agreement of finite element solutions of specific, well-characterized benchmark problems. Uncertainty in solutions are characterized with respect to: software platform, element type, degrees of freedom, and element aspect ratio.

Publications

• Patrone, P. N., Dienstfrey, A., "Uncertainty Quantification in Molecular Dynamics", Reviews in Computational Chemistry, invited review to appear 2017.
• Patrone, P. N., Rosch, T. W., Phelan Jr., F. R., "Bayesian Calibration of Coarse-Grained Forces: Efficienty addressing transferability", J. of Chemical Physics 144, 154101 (2016),  http://dx.doi.org/10.1063/1.4945380(link is external)
• Patrone, P. N., Dienstfrey, A., Browning, A. R., Tucker, S., Christensen, S., "Uncertainty Quantification in Molecular Dynamics Studies of the Glass Transition Temperature", Polymer 87, 22 (2016), http://dx.doi.org/10.1016/j.polymer.2016.01.074(link is external)
• Fong, J. T., Filliben, J. J., Heckert, N. A., Marcal, P. V., Rainsburger, R. and Ma, L., "Uncertainty Quantification of Stresses in a Cracked Pipe Elbow Weldment Using a Logistic Function Fit, a Nonlinear Least Square Algorithm, and a Super-Parametric Method", Procedia Engineering 130, (2015), http://dx.doi.org/10.1016/j.proeng.2015.12.183(link is external).
• Dienstfrey, A., Phelan Jr., F. R., Christensen, S., Strachan, A., Santosa, F., Boisvert, R., "Uncertainty Quantification in Materials Modeling", JOM 66, 7 (2014), http://dx.doi.org/10.1007/s11837-014-1049-1(link is external)

Short courses and Conference Presentations

• The short course, "Uncertainty Quantification (UQ) in Finite Element Method (FEM)" was offered at NIST on Dec 7, 2016. Course materials are available upon request.
• Fong, J. T., Filliben, J. J., Heckert, N. A., Marcal, P. V., and Cohn, M. J., 2016, "A Statistical Approach to Estimating a 95% Confidence Lower Limit for the Design Creep Rupture Time vs. Stress Curve when the Stress Estimate Has an Error up to 2%," in Proc. ASME 2016 Pressure Vessels & Piping Conf., July 17-21, 2016, Vancouver, BC, Canada Paper No. PVP2016-63350 (2016), http://dx.doi.org/10.1115/PVP2016-63350(link is external)
• The Uncertainty Quantification in Materials Modeling(link is external) workshop was held at the National Center for Nanotechnology, Purdue University, July 28--31, 2015.