Tunable Compression of Wind Tunnel Data

Summary

Measurements of pressures exerted by wind on buildings, as are made in wind-tunnel tests involving model buildings instrumented with pressure taps, are an invaluable resource to design safe buildings efficiently. However, the very large volumes of data that such tests typically generate pose a challenge to their widespread use in practice. To facilitate such use, we propose a scheme that achieves very high compression rates with negligible signal distortion, and that also allows incremental data transmission to meet variable engineering requirements.

The data used in this study consists of measurements of pressures at 18 taps placed along the center bay of a low-rise building model, made in the wind-tunnel of Ruhr-Universität Bochum (Bochum, Germany), acquired at 1 600 Hz, over 100 time periods equivalent to 1 full-scale storm-hour each, all with the same wind-flow direction. The bending moments at two knees of the structure drive the engineering design.

Description

Variability of Bending Moments

The values of the bending moments vary both within each run, and between runs. The between-runs variability provides a standard against which one should assess the severity of any loss of information that a data compression scheme may incur. To assess it, we fitted a linear, Gaussian mixed-effects model to the 15% trimmed mean of the values of the bending moment over each interval of duration 1 full-scale minute (which comprises 819 measurements), at each knee of the frame separately. The fits were done using function lme of the nlme package for the R environment for statistical computing. The between-run, relative variability of the maximum absolute value of the bending moment over the same 1 full-scale minute intervals, amounted to 5.5%.

Since there are contributions from other, additional sources of uncertainty in play (for example, analog-to-digital converter, measurement of the reference pressure, geometrical location of the taps), errors of this magnitude that the compression may induce are quite acceptable.

Compression

A wavelet representation for the time series of pressure measurements acquired at each tap can be used to compress the data drastically while preserving those features that are most influential for engineering design. The loss incurred in such compression is tunable and known.

In this case, we used the discrete wavelet transform computed with Daubechies' least asym­metric wavelet LA(20) (which we chose by cross-validation), with 1 "smooth" and 9 levels of "detail", and periodic boundary conditions, together with the following simple, quantile-based thresholding rule to annihilate wavelet coefficients: given a target compression rate 100(1 - a)%, for some 0 < a < ¼, define G as the 100(1 - 2a)th percentile of the absolute values of the wavelet coefficients, and set all wavelet coefficients to 0 whose absolute value is less than or equal to G.

Major Accomplishments

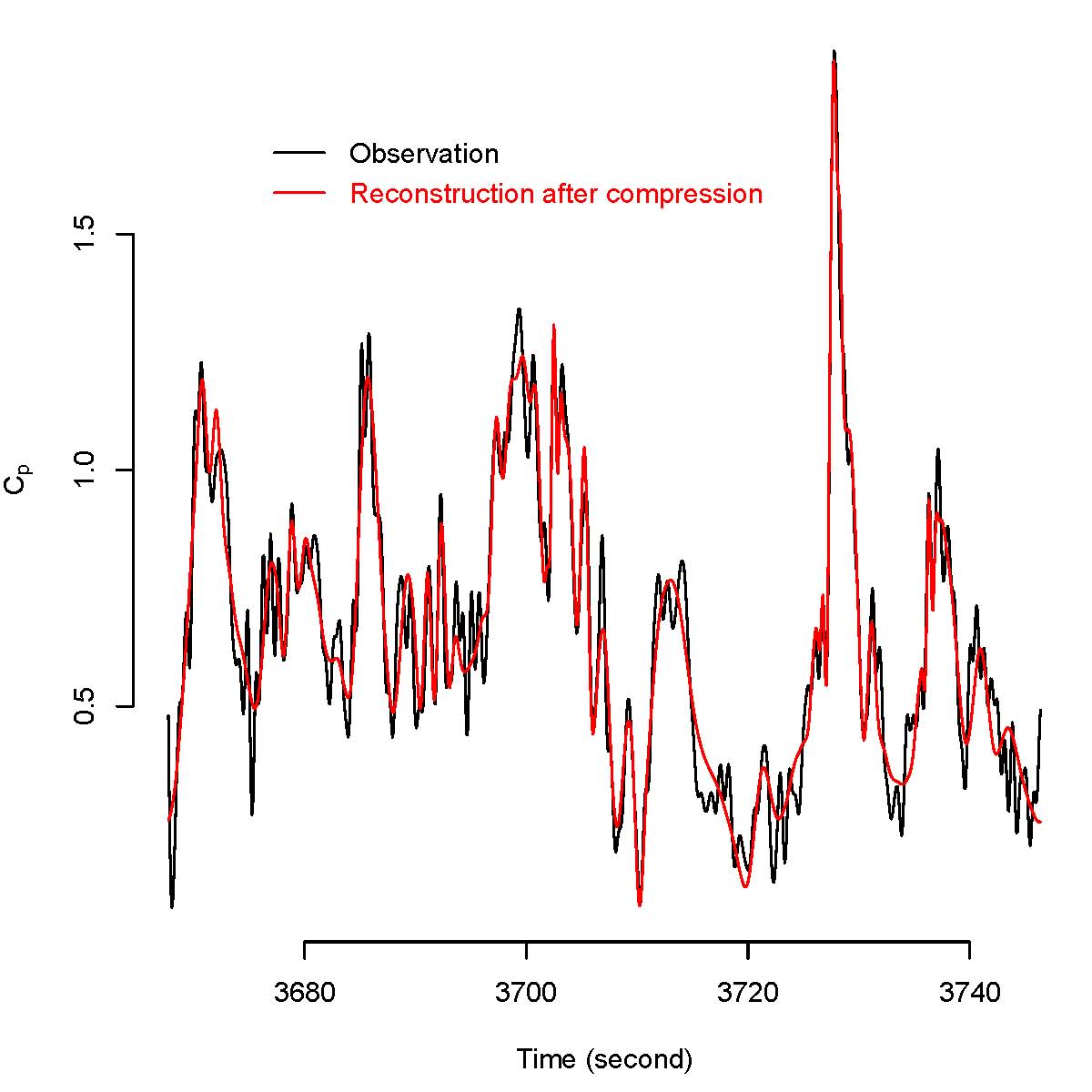
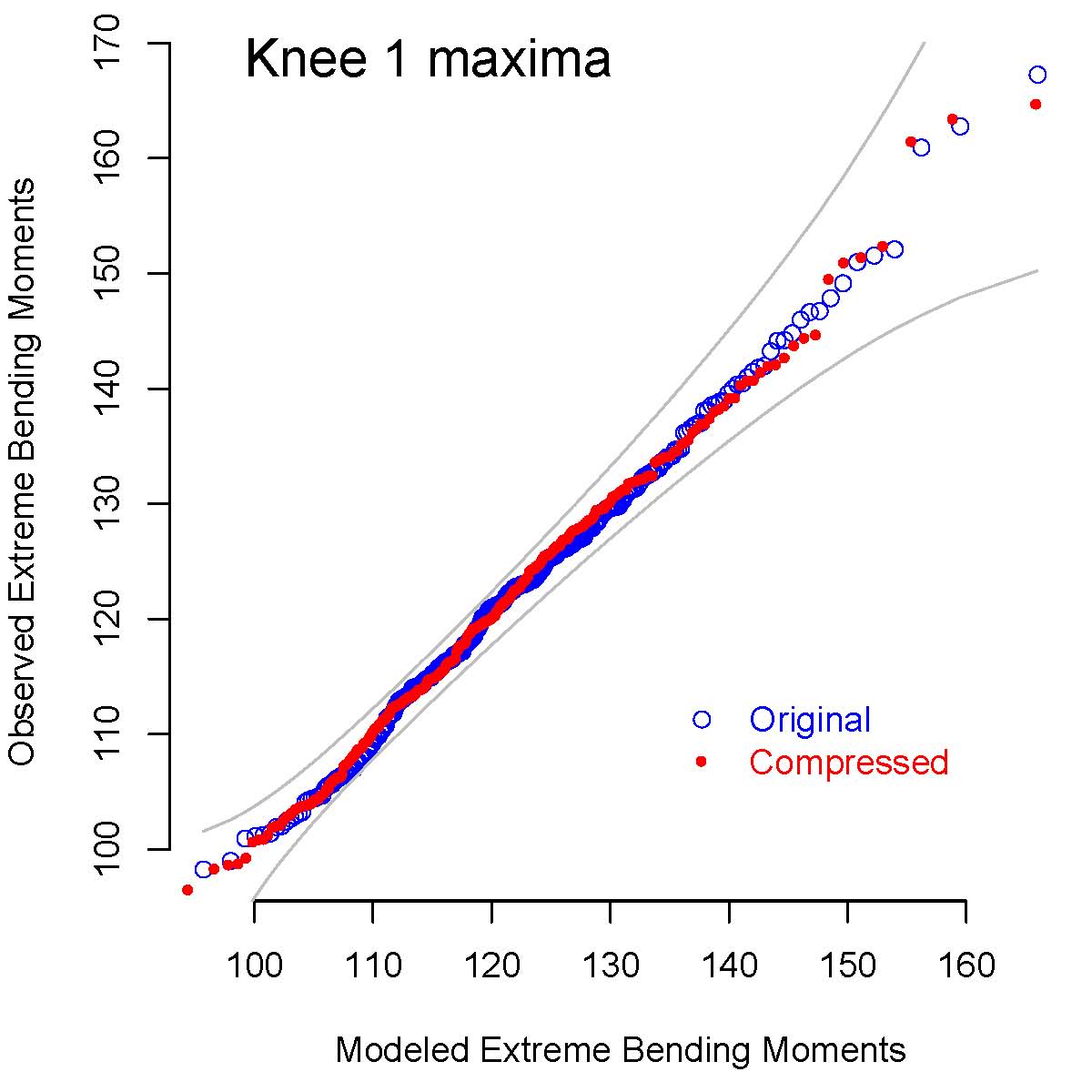
Figure 1 shows the distortion induced by 90% compression of the series of pressures measured at one particular tap, and compares the extreme values of the bending moment at one knee of the structure before and after compression: 98% of the extreme moments corresponding to compressed data differ by less than 5.5% from their counterparts computed from the original data; furthermore, the sample of extreme bending moments after compression is statistically indistinguishable from a sample drawn from the generalized extreme value distributed fitted by maximum likelihood to the extreme moments corresponding to the original pressures.