DFT Benchmarking

Summary

DFT is a widely used computational technique in the material science community and it provides interpretative tools for understanding experimental results as well as reference data to use/fit to for other computational methods. However DFT results depend on the particular DFT realization that was chosen to perform the calculation (for instance, which exchange term, which correlation functional, which approximate form for the wave function). This means that different “parameterizations” (numerical values for actual parameters as well as functional forms for the approximated terms etc.) produce different values for the same physical quantity. Such a spread in results, intrinsically constitute a computational-method-related uncertainty, and such an uncertainty should be reported together with every DFT-computed data. The  goal of this  work is to perform an extensive evaluation of such uncertainties by computing basic physical quantities using many DFT codes as different from one another as possible and, for each code, using several choices for all other parameters.

Description

Since its inception exactly 50 years ago this year, density-functional theory (DFT) has evolved from an exotic idea of physicists into the most-widely used tool for the computational prediction of materials’ structures and electronic, optical, magnetic, and mechanical properties. While DFT presents an in-principle exact theory, various approximations are required to perform practical DFT simulations. These approximations can be classified into two categories: (i) controlled approximations, whose errors can be made arbitrarily small through adjustable parameters typically at the expense of increased computational cost, and (ii) uncontrolled approximations, whose errors are unknown exactly. The controlled approximations include the basis set approximation, e.g. plane-wave, spline, or local orbital representation, for the Kohn-Sham orbitals, the k-point sampling for periodic systems, the choice of pseudopotentials, and the numerical parameters for convergence and integrations. The uncontrolled approximation in DFT is the choice of exchange-correlation functional. The ubiquity of available DFT codes  and the resulting increasing use of DFT for materials property predictions by experts and non-experts alike, demands a careful assessment of the effects of the various approximations on the accuracy of materials predictions. Also an assessment of the numerical correctness of the results from different DFT codes is highly desirable. These are the main goals of the proposed effort.

Major Accomplishments

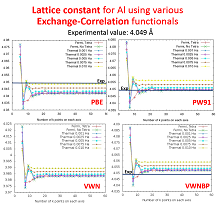
• Investigation the convergence of important physical quantities like lattice constant and bulk modulus as afunction of k-points and smearing;
• Computation of lattice constant, elastic constants, and relative energies for single elements in various structures (fcc, bcc, hcp, sc, diam, ..) using various exchange-correlation functionals.