Controlling collisions between laser-cooled atoms using magnetic fields and nano-eV colliders

Summary

We investigate collisions of atoms in either micro-Kelvin gasses or in nano-colliders, where two small atomic clouds are made to collide with adjustable energy up to an energy equivalent of 1 mK. This is achieved with theoretical simulations and comparisons to experimental data. We focus on understanding resonant phenomena, so-called Verhaar-Fano-Feshbach resonances, in collisions among laser-coolable alkali-metal and lanthanide atoms in magnetic fields. Recently, researchers realized that the distribution of the magnetic-field locations of these resonances is chaotic for magnetic lanthanide atoms dysprosium, erbium, and thulium indicating the complexity of the interactions among such atoms.

Description

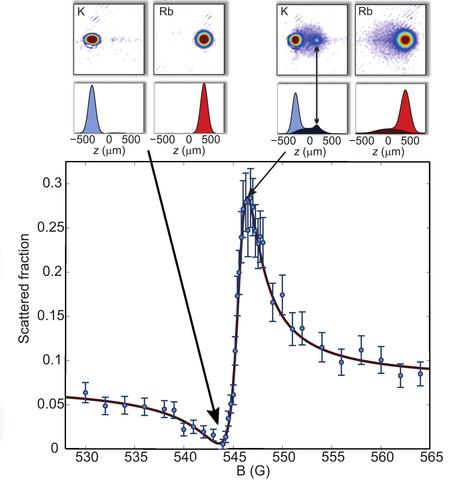
A Verhaar-Fano-Feshbach resonance in the collision of a potassium (K) and rubidium (Rb) atom as measured with the nano-eV atom collider of N. Kjærgaard at the university of Otago, New Zealand. Measured are the number of scattered atoms (markers with standard uncertainty) as a function of magnetic field using 1 μK potassium and rubidium clouds with a relative collision energy E such that E/k=52(1) μK.  The solid curve is a Beutler-Fano lineshape, whose parameters were found from a fit to the experimental data. The images above the graph show measured K and Rb densities profiles after the clouds have passed through each other at magnetic fields, where the scattered atom fraction is smallest and largest, respectively. Both scattered and unscattered atoms are visible. (Adapted from Thomas et al., Nature Comm. 9, 1 (2018).)

Understanding collisions between atoms is important to many research efforts at NIST. Atomic clocks based on cesium or rubidium atoms at microkelvin temperatures, for example, are measurably affected by atom-atom collisions. So much so that in a candidate next-generation atomic clock, now based on optical transitions in alkaline-earth atoms, the atoms will be prevented from colliding. Experiments aiming to simulate quantum-phase transitions with gasses of cold atoms, however, would not have been successful without collisions. Examples are the formation of Bose-Einstein condensates and the observation of superfluid Cooper pairing of fermionic atoms.

The relevant observables for these and other experiments can be theoretically determined from elastic, momentum-changing collisional processes. Elastic collisions lead to shifts in the atomic transition energies used in atomic clocks and control the time scale over which gasses approach thermodynamic equilibrium.  At ultra-cold temperatures, typically defined as temperatures below 1 mK, quantum physics and the wave nature of atoms determines the behavior of these observables and classical descriptions fail. 

Resonances also occur in the elastic collisions of ultra-cold atoms. Here, they correspond to rapid changes in the cross section (or effective size) of the atoms as a function of an applied magnetic field as well as collision energy. The figure on this page shows an example of a so-called Verhaar-Fano-Feshbach resonance in an approximately k × 50 μK collision of a cloud of 1-μK potassium atoms and a cloud of 1-μK rubidium atoms as measured with the nano-eV atom collider of Dr. N. Kjærgaard at the University of Otago, New Zealand. Here, k is the Boltzmann constant. We are currently investigating how we can further understand and make use of resonances using ultracold-atom colliders.

In ultracold gasses of dysprosium and erbium, lanthanide species with for atoms large magnetic moments, the density of resonances as function of magnetic field is exceptionally high over magnetic field strength ranges that are easily achievable in laboratory experiments. In fact, the distribution of resonances seems chaotic. Theoretically, we have only been able to reproduce and explain the mean resonance density and other “simple” statistical properties of the distribution based on a simplified model of the interactions among the magnetic lanthanide atoms. A quantitative understanding of the resonance positions is still missing.