Summary
A Complex System is any structure, process, organization, or organism characterized by a large number of interconnected components whose micro-interactions lead to macro-behavior which is nonlinear and/or non-predictable. Examples of complex systems include the physical (earthquakes, avalanches,forest fires), the biological (ant colonies, slime molds, humans), the social (cities, economies, transportation networks), and the informational (compute grids, web services, the internet). The ITL Complex Systems Program in general seeks to understand the fundamental science of these systems and develop rigorous descriptions (analytic, statistical, or semantic) that enable prediction and control of their behavior. The specific programmatic motivation was that there was "no science today (2006) that offers the fundamental knowledge necessary to design large complex networks so that behaviors can be predicted prior to building them" (Network Science, 2006 NRC Report).
The particular complex system application reported on here focuses on a system dealt with on a daily basis, namely, the internet. In particular, the goal of the study was 3-fold:
1. to quantify (and understand) internet congestion by determining the relatedness of 22 selected response factors,
2. to assess the sensitivity of such responses to 11 usage and environmental factors, and
3. to intercompare the relative performance of various (7) Congestion-Control algorithms (TCP and beyond).
Highly efficient fractional factorial experiment designs were constructed and a battery of custom data analysis graphics were assembled and applied.
Description
Complex systems are generically characterized by a large number of factors and a large number of potential responses, hence statistical questions immediately present themselves as to
1. What should be measured?
2. What experiment design should be used to generate content-full data?
3. How should such data be analyzed? and
4. How should such statistical analysis results be interpreted and translated into system insight, understanding, & predictability
Framework: In practice, the generic 5-step statistical approach as illustrated in has provided the framework for many advances in NIST physical science projects--in characterization,modeling, sensitivity analysis, optimization, validation, etc.--and so it was not surprising that this same general framework did in fact provide the structure, the "roadmap", and the methodology to address the complex information science problem at hand. Further, since complex systems may be viewed from a statistics point of view as simply a multi-response, multi-factor, time series, then tools from all three of these areas may be borrowed and applied.
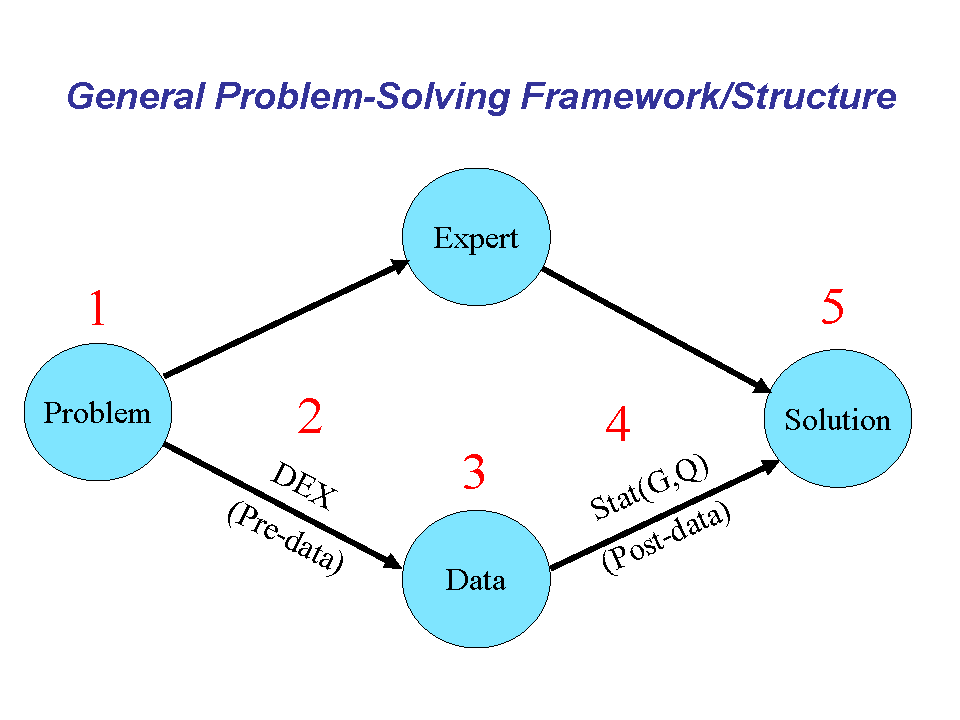
Problem: Component 1 in the framework is to enumerate specific questions that the study will address . Some of the specific questions (and experiments) of interest addressed in the project are:
Q1. What are the important factors that influence internet congestion?
Q2. Do these factors interact?
Q3. Can the common internet congestion-control algorithm TCP be improved on?
Q4. Which is the best among the half-dozen or so proposed (by IT researchers at various institutions) competitors for TCP?
Q5. Under what conditions?
Q6. Are our conclusions robust over network parameter and user conditions?
An added bonus from the statistical framework for this project was that it also served to provide an answer to the validation question:
Q7. Are the local NIST/ITL internet simulation models (= programs) adequate?
(The answer was yes, but some important glitches were uncovered with the net effect that the simulator itself is now improved).
Experiment Design: Component 2 (experiment design) in the 5-step framework played a particularly important role. It allowed for a common vocabulary, it provided a simplifying 2-element structure:
k = # factors = ?, and
n = affordable number of internet experiments = ?),
it forced the specificity of purpose required to translate any of the large number of possible internet questions into the specific, concrete question that the "next experiment" was going to address, and it took advantage of the interactive statistical process of starting with an amorphous problem with an "endless" number of (mostly continuous) factors and converging to a finite, workable, scientifically-prioritized subset of factors with well-defined discrete settings. It also opened up a new way of thinking about this IT problem, and a new, powerful tool at the disposal of the scientist, namely the orthogonal fractional factorial experiment design, by which the IT scientist may efficiently, effectively, and systematically probe an information system as complex as the internet. The experiments were carried out by internet simulation programs run on a battery of computers. To carry out a single simulation run required considerable "wall clock" time. The project testing became feasible only by combination of the following 2 tools (one statistical and one computational):
1. the fractional factorial experiment designs which reduced the decades' worth of running into a year; and
2. the use of 48 processors which reduced the year's worth of processing into a week.
Both components were critical.
Data Analysis: Furthermore, the necessities of dealing with a large (15 to 50) number of responses--each one sensitive to a different aspect of internet behavior--led to the design and application of a variety of custom graphical data analysis techniques to extract from the multi-factor/multi-response data the maximal amount of underlying structure and insight into primary factors and interactions alike (see figures 2 and 3).
In addition, the method outlined in this paper was repeated in each of our experiments, where we exercised each congestion control mechanism under 32 conditions that were spread throughput the parameter search space in an orthogonal and balanced fashion. (We have proposed a case study based on this method for presentation at the 2010 Winter Simulation Conference.) NIST-906588 "Comparison of Two Dimension-Reduction Methods for Network Simulation Models"(Kevin L. Mills and James. J. Filliben) discusses two different approaches we used to reduce the response space in our experiments. In this particular paper we reduced a 22 dimensional response space to 4 (using one method) and 7 (using a second method).
The goal of response space reduction is to identify the most important aspects of our model's behavior, which allows us to represent those aspects in a complete and balanced way within our experiments.(We have proposed a case study based on this method for presentation at the 2010 Winter Simulation Conference.) The main power of the methods we used arises from 2-level, orthogonal fractional factorial (OFF) experiment designs (NIST-904961), which allow us to vary all experiment parameters simultaneously while probing the search space widely in a balanced fashion. This leads to broader insights for lower computational cost than the one factor-at-a-time (1-FAT) experiment designs that are typically adopted by network simulation practitioners. In addition, the broader insights provided by OFF experiment designs can reveal areas that might be profitable to study with FAT designs.
While the design and analysis methods described here were utilized to study specific internet congestion-control mechanisms, the methods are in fact quite general and can be applied to many experiments that require simulating a complex search space that is otherwise deemed to be computationally infeasible. In fact, we are currently (12/10) using similar such methods to investigate resource allocation algorithms that might be used in Cloud Computing.
Major Accomplishments
This project has resulted in an significant amount of insight about the relative merits of various internet congestion-control algorithms, what traffic factors affect algorithmic performance, and what interactions between factors affect relative performance. The IT results and the Stat methodology for modeling and analyzing global behavior has generated considerable interest in the IT measurement science community.
We have produced three technical papers:
"A Study of Proposed Congestions-Control Mechanisms"(Kevin L. Mills and James. J. Filliben) describes in detail (500 pages) all of the details involved in the experiment design, the simulation, and the data analysis for this project. This appeared as a NIST Special Publication SP 500-282.
NIST-904682 "How to Model a TCP/IP Network using only 20 Parameters"(Kevin L. Mills and James. J. Filliben) describes the reduced-parameter simulation model that we constructed to use for our study. Using this reduced-parameter model enabled us to reduce the computation requirements for our experiments. (A slightly shorter version of this paper will be presented at the 2010 Winter Simulation Conference.)
NIST-904961 "An Efficient Sensitivity Analysis Method for Network Simulation Models" (Kevin L. Mills and James. J. Filliben) describes our method to identify those parameters/factors (from among the 20 in our model) that produced the most significant changes in model responses. We could base further experiments in our study on this subset of parameters, which would further reduce the computational requirements needed to conduct our simulations.

