New Telecom Receiver System Checks Reliability of Message Components in Real Time

Scientists at the National Institute of Standards and Technology (NIST) have invented and demonstrated a novel scheme for substantially improving the detection accuracy of information transmitted in pulses of light through telecommunications systems such as the Internet. The “smart” quantum receiver system continuously estimates the reliability of the signals it measures, making error correction easier and more efficient.

Errors are endemic. The signal strength of messages traveling as streams of photons– the smallest individual units, or quanta, of light – inevitably grows feeble when photons are lost as they travel long distances in optical fibers. In addition, because photons are quantum objects, measuring their properties entails some unavoidable amount of uncertainty.

At the receiving end of the line, the paramount questions are: What have I measured and how confident can I be that my measurement of a message unit is accurate? How much error can I tolerate and still understand the message? (Imagine a string of words in which all the vowels were missing. t mght stll b ndrstndbl.) And what is the maximum achievable accuracy?

The NIST method, developed with colleagues at the Joint Quantum Institute and published January 25 in Physical Review Letters, addresses those questions by determining which parts of a message measurement are most likely to be accurate and which are less so, and labeling each part accordingly.

“Suppose you are receiving a message using an ‘alphabet’ of four different symbols: A, B, C, and D,” said NIST senior project scientist Sergey Polyakov. “In our system, each symbol now comes with an additional quantitative label: ‘I am pretty reliable’, ‘I am likely to be A or B, but probably not C or D’, or ‘I am not sure’. So before we share the received message with the end-user, we know exactly which symbols we can trust and which need to be corrected.”

Measuring Phases

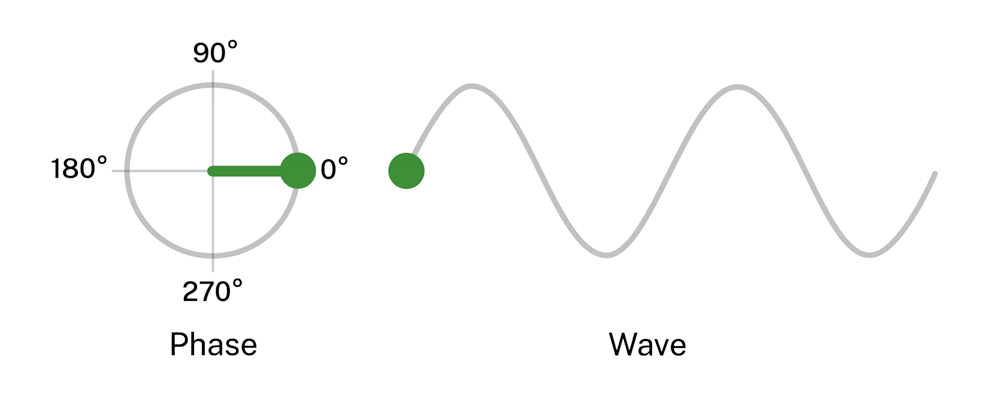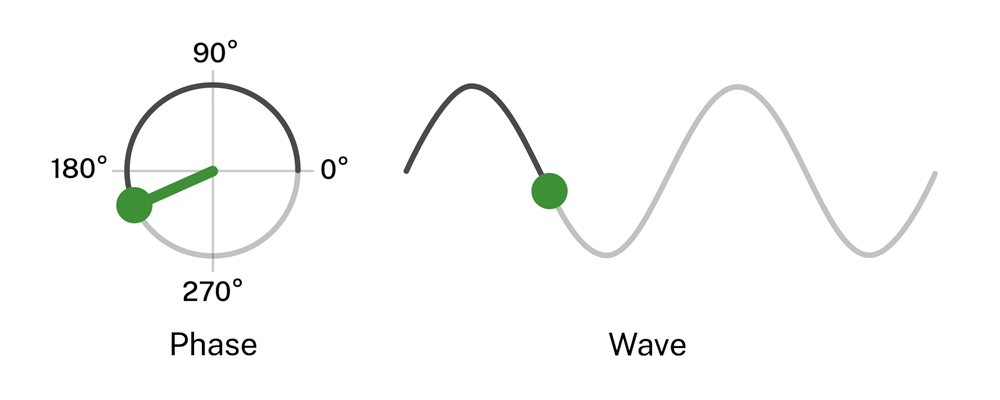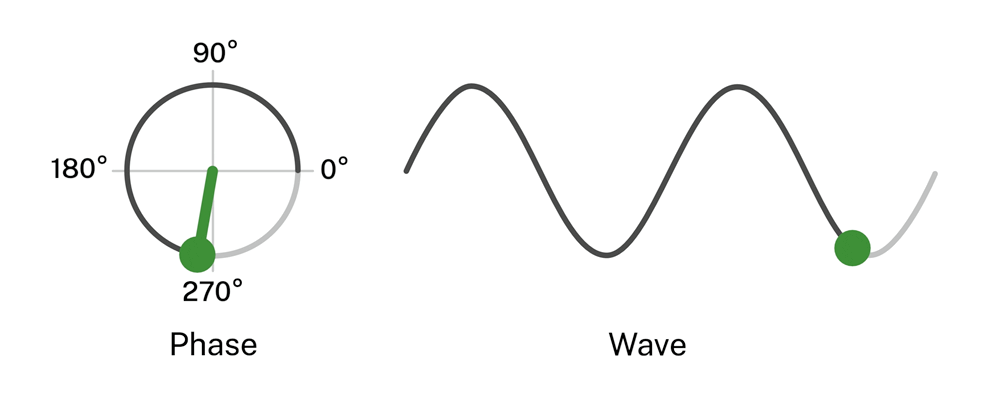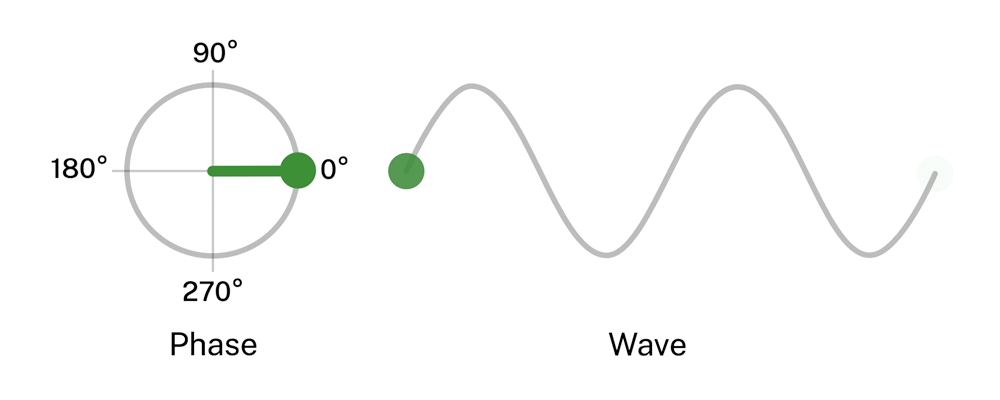
All electromagnetic communications systems convey information by changing (modulating) some aspect of a carrier wave. In amplitude modulation (as in AM radio), the message is encoded as varying strengths of the wave pulses. In frequency modulation (FM), it’s encoded as changes in the frequency. In many modern optical telecom systems, information is encoded by changes in phase – modulating the starting point on a wave pulse where the information is placed. Due to channel losses, the incoming signal arrives in weak pulses, each of which contains a small number of identically coded photons.

In the NIST experiment, the laser generating the message was set to produce very few photons per pulse – an average of about three over a pulse duration of approximately 60 millionths of a second – approximating a signal highly attenuated in fiber transit. The photons in each pulse were modulated in four phases (see Figure 1), although different numbers are possible.

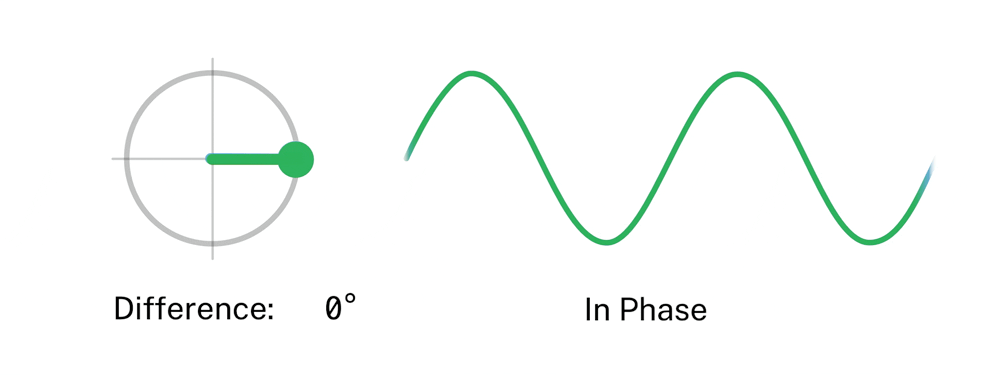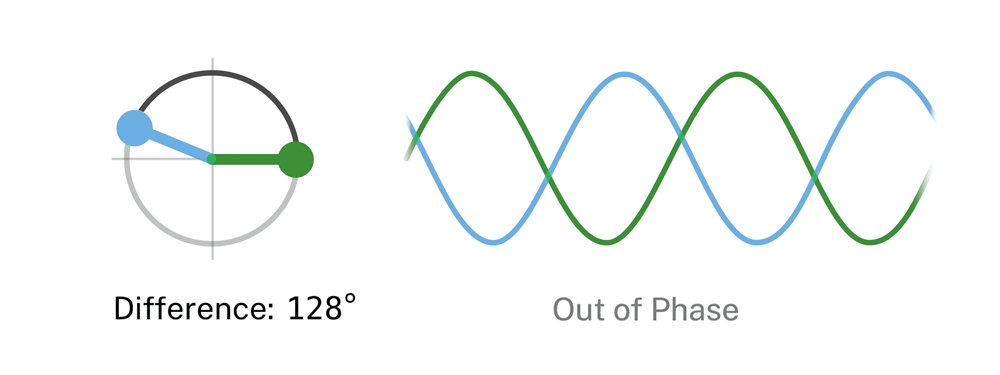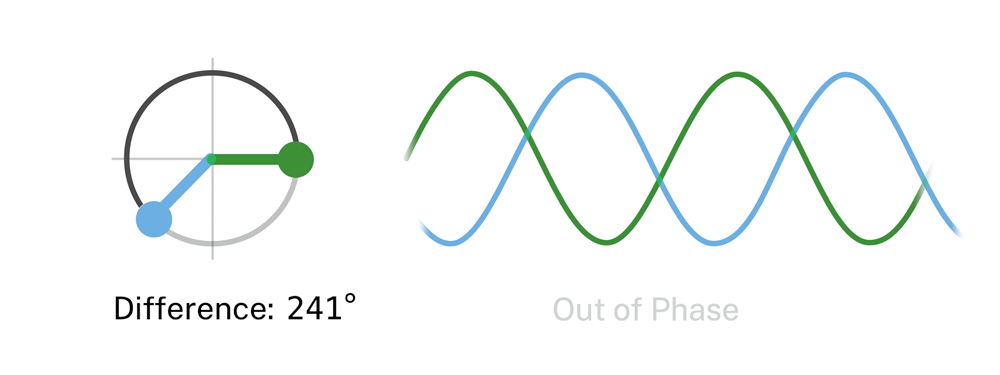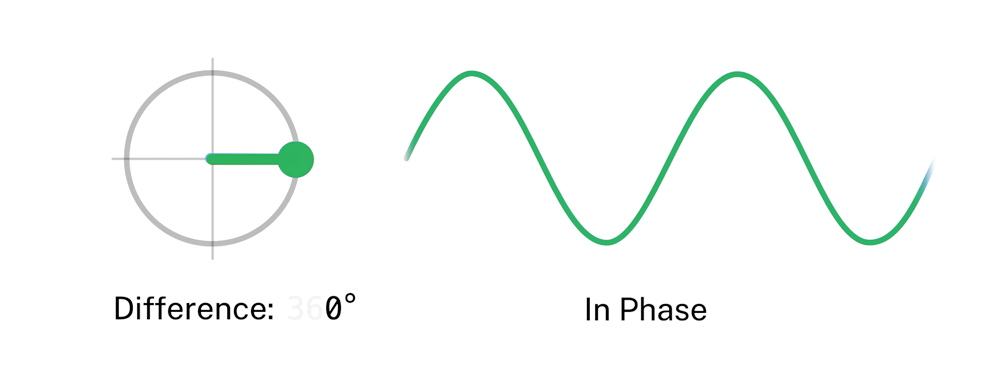
After entering the receiver, the signal pulse passes through a beam splitter. (See animation.) As it does, it is combined with a “reference” pulse generated by a laser in the receiver. The reference pulse is also encoded with one of the four possible phases. If the phase of the reference pulse is the same as the phase of the incoming signal, the two cancel each other out and no light registers at a detector on the other side of the beam splitter. That absence of light constitutes determination of the signal phase. (Of course, because the detector does not fire, the observer has no direct evidence of that.)

Quantum Phase Detection

If the phase of the reference pulse does not match the phase of the signal, the signal pulse is not canceled and passes into the detector. When the detector registers the photon, that is strong evidence that the phase of the reference pulse did not match the phase of the signal pulse, and it prompts the system to change the phase of the reference pulse to the next most likely phase.

That new reference pulse is routed to the beam splitter to interact with photons remaining in the signal pulse. If the phases again do not match, the detector registers light and the system shifts the phase of the reference pulse again, and so forth. Each non-match increases the probability that a different phase is correct, reaching high certainty. However, no practical measurement can be 100 % certain due to experimental deficiencies.

“As measurements continue until the input signal pulse is exhausted,” said JQI/NIST researcher Ivan Burenkov, first author on the new article, “our estimates of the probability that the input pulse has a particular phase continuously change during each measurement. We expect really few photon detections because the signals are weak. So, when we send a reference and receive no photons at the detector, we don’t know for certain whether the guess is correct and the photons in the incoming pulse were canceled or whether the guess is incorrect, but a photon did not get detected just yet.

“Immediately after sending the reference, we learn little because we don’t have much new evidence. But the longer we don’t receive a photon at the detector, the more likely it is that the input has been completely canceled and our degree of confidence grows as we accumulate photon detections. After each photon detection, we not only update the probabilities but also the reference wave.”

That sort of updating is called Bayesian inference, in which the probability of an outcome is constantly recalculated as more information arrives. The result is a record of measurements with an associated uncertainty for each.

This makes error correction much more efficient because it identifies which specific parts of a message are probably right and which are most uncertain. “Suppose,” Polyakov said, “you received the words ‘We need sant.’ What was actually meant? In the absence of any guidance, you don’t know how to correct it.

“But if you knew that the confidence in the first three letters was fairly high and the fourth was highly uncertain, you could assume that the intended word was sand. Or if you knew that the third was highly uncertain and the other ones somewhat more probable, you’d come up with salt.

“In many cases, you wouldn’t need to contact the sender and ask for another transmission. You could just create a sophisticated algorithm based on your calculated confidence levels and do the error correction on your end.”

The better a receiver’s error detection and correction system, the less energy is needed for accurate communication. “Or,” said NIST guest researcher M.V. Jabir, “it could mean that if previously I could communicate at a distance of 100 miles, with a better receiver I could go 200 miles.”

Paper: Ivan A. Burenkov, N. Fajar R. Annafianto, M. V. Jabir, Michael Wayne, Abdella Battou, and Sergey V. Polyakov, Experimental Shot-by-Shot Estimation of Quantum Measurement Confidence. Phys. Rev. Lett. 128, 040404 – Published 25 January 2022. DOI: 10.1103/PhysRevLett.128.040404