Official websites use .gov
A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.
The heart of the torsion balance. This section (above: top view, below: side view) hangs from a thin copper strip, enclosed within the tall central pillar capped with mirrors. The four copper cylinders are the inner masses. Outer masses not shown.
If you spend time in physics research circles, you may have heard of the big G controversy.
The universal constant of gravitation, G – affectionately known as “big G” to distinguish it from little g, the acceleration due to Earth’s gravity – is a fundamental constant of nature. It completes the famous equation that describes the gravitational force of attraction between any two objects in the universe, whether they are planets or people or office supplies.[i]
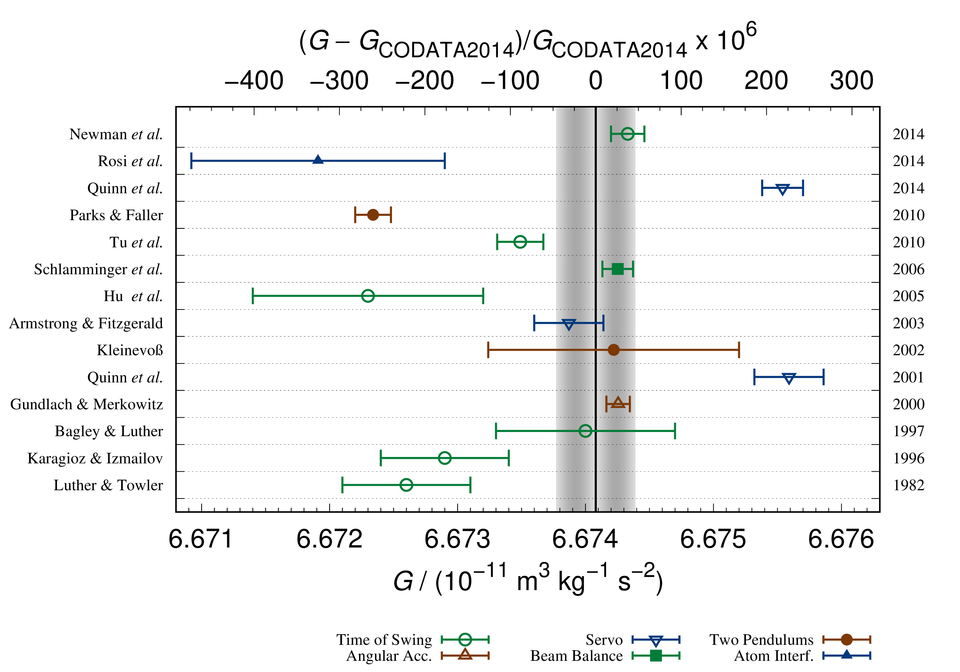
Scientists have been trying to understand the strength of gravitation since Isaac Newton first identified the relationship between masses and gravitational force more than 300 years ago. But despite centuries of measurement, the constant is still only known to 3 significant figures, much less than any other constant of nature. The mass of the electron, for example, is known to about 8 digits.
Furthermore, as G measurements become more and more sophisticated, rather than converging on a single value, the results diverge maddeningly from each other, with error bars that do not generally overlap.
“Big G has been a frustrating problem,” says Carl Williams, Deputy Director of NIST’s Physical Measurement Laboratory (PML). “The more work we do to nail it down, the bigger the divergences seem to be. This is an issue that no metrologist can be pleased with.”
Despite the lack of convergence, most of these disparate results are starting to cluster around one value. But there are some noticeable outliers, such as a pair of well-respected experiments conducted over the past 15 years by the International Bureau of Weights and Measures (BIPM), the intergovernmental organization that oversees decisions related to measurement science and standards.[ii]
“There’s sort of a big debate: Is it that we don’t really understand gravity as a theory?” says NIST postdoctoral guest researcher Julian Stirling. “There’s some small chance that maybe our understanding of gravity is wrong and there’s something slightly different about these experiments that causes the value to be different from other big G experiments, which would be really interesting.”
The less exciting but more likely answer though, he says, is that systematic errors have crept into the BIPM measurements. So two years ago, the BIPM scientists and other leaders in the worldwide efforts to measure big G met and decided that these tests should be conducted again with the same equipment, but at a different facility and with a different team.[iii]
NIST researchers took on the challenge and are currently preparing to repeat the BIPM experiment using the original apparatus, with a few upgrades.
The Torsion Balance
G is difficult to measure in part because it is extremely weak compared to other fundamental forces. Its value is tiny, about 6.67 x 10-11 m3 kg-1 s-2, a trillion trillion trillion times weaker than the electromagnetic force.
“The gravitational force between two sedans parked one space apart is approximately 100 thousand times weaker than the force to separate two post-it notes,” Stirling says. “There’s a reason why this is the least well known of all the fundamental constants.”
To suss G out, the BIPM experiment used a torsion balance, a popular method for measuring G and one that was used in the very first measurements by English scientist Henry Cavendish in 1798. This type of device works by measuring the gravitational force between relatively small masses, typically metal spheres or cylinders that you could hold in your hand, by gauging the twisting or torqueing of a wire or strip of metal.
BIPM’s version is much more sophisticated than the original Cavendish balance. It uses eight masses, cylinders made of an alloy of copper and tellurium. Four are sitting on a round carousel that can be rotated between measurements.[iv] Inside the carousel, the other four masses, slightly smaller, sit on a disk suspended from the top of the balance by a strip of copper-beryllium 2.5 mm wide and 160 mm (approximately 6 inches) long, with about the thickness of a human hair.
When the outer masses are placed so that they are exactly even with the inner masses, there is equilibrium. However, when the outer masses on their carousel are turned to a new orientation, the inner masses feel a net pull toward them. The gravitational force causes the inner masses to migrate toward the outer masses, twisting the strip that suspends them. Earth’s gravity does not affect the measurements, since the attraction between the masses happens perpendicular to the planet’s gravitational pull.
The amount of force needed to twist the strip a certain amount is known. So by measuring the physical distance that the inner masses travel toward the stationary outer masses, using laser light and a mirror at the top of the strip, scientists can calculate how great the gravitational attraction is between them. And, with that information, they can fill in the gaps in Newton’s gravity equation to calculate big G.[v]
Real-time Dimensional Measurements
Of course, to measure big G researchers also need to measure the other quantities in Newton’s gravitational equation. That means knowing the exact mass and location of all of its parts, “every hole, every mass, and every screw,” Stirling says. And that requires a coordinate measuring machine (CMM).
CMMs are used to measure dimensions with high accuracy. This particular CMM is an immense granite table with an overhead touch probe, which will be used to detect the distances between points on an object in three dimensions with potentially half a millionth of a meter measurement uncertainty.
The individual pieces of the torsion balance will be probed by a CMM before the experiments begin. But the CMM will also be used during the actual experiment, to ensure that the distances between the cylinders are known to high accuracy. Each big G measurement takes place in vacuum, so only the outer cylinders are accessible with the vacuum cap on.
At the moment, the team is still preparing for their experimental run. This summer, a new CMM was delivered to NIST that was large enough to be used for the experiment. In fact, the CMM was so big that it had to be lowered in pieces through an air vent above the laboratory level, about four stories below ground, and a wall had to be removed to get it into the measurement room.
Though the hardware is all from BIPM, there are a few updates. “We’ve had to replace a lot of the electronics,” Stirling says. “And also computers have changed a bit over the last 15 years.”
“We are extremely excited, and also a little terrified, to see if we can sort out this discrepancy, and convincingly identify the measurement bias or unaccounted-for physics -- or perhaps even new physics -- that explains the existing results,” says Jon Pratt, Chief of PML’s Quantum Measurement Division. “The terrifying part is obvious: bias or unaccounted-for physics in this experiment is far and away the most likely explanation, yet they will be extremely hard to find, since some of the best measurement scientists in the world have already done their best to eliminate them! The exciting part for us is maybe less obvious: simply put, sorting out this type of discrepancy is what science is all about, and kind of what we live for at NIST.”
Measurements will begin this winter.
Reported and written by Jennifer Lauren Lee.
[i] Calculating the gravitational attraction between two objects requires taking the product of two masses and dividing by the square of the distance between them, then multiplying that value by G. The equation is F=Gm1m2/r2.
[ii] The recommended value for G is set by CODATA, the International Council for Science Committee on Data for Science and Technology, which analyzes the results of individual experiments and provides an internationally accepted sets of values for fundamental physical constants. CODATA's latest set, released in 2014, recommended a value for G of 6.674 08(31) x 10-11 m3 kg-1 s-2, where the number in parentheses indicates uncertainty in the final two digits.
In contrast, the BIPM experiment’s most recent result, published in 2013, found a relatively large value for G at 6.675 45(18) × 10−11 kg−1 m3 s−2, with a relatively narrow error bar.
[iii] For more information about the international push to measure the gravitational constant, see “Trouble with a Capital ‘G’”
[iv] The BIPM experiment moved the outer masses between measurements and then gauged how much the inner masses had shifted each time. The NIST team plans to do something slightly different, by rotating the outer masses very slowly by a full 360 degrees and monitoring the torque constantly.
[v] There is actually a second mode that allows researchers to use electrodes to prevent the inner masses from moving. The masses still feel a gravitational force, but that force is counteracted by an electrostatic force that can be measured. Having two different modes yielding similar answers makes researchers more confident in their results.