Official websites use .gov
A .gov website belongs to an official government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.
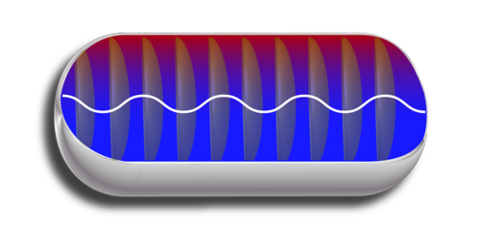
Schematic diagram of a gas-filled pressure vessel. The red-to-blue shading represents the temperature gradient in the gas, with the higher (red) temperatures near the top. The ovals represent a standing sound wave; its frequency is mostly determined by the average temperature of the gas. The wavy line represents a resonant electromagnetic wave; its frequency is mostly determined by the length of the tank. Wavelengths are not to scale.
Scientists at the National Institute of Standards and Technology (NIST) have developed a novel method to rapidly and accurately calibrate gas flow meters, such as those used to measure natural gas flowing in pipelines, by applying a fundamental physical principle: When a sound wave travels through a gas with regions at different temperatures, the sound wave's average speed is determined by the average temperature of the gas.
Accurate calibrations of gas flow meters issues are of urgent interest to meter manufacturers and calibration labs, and potentially impact all segments of the natural gas industry.
Conventional calibrations are typically conducted by flowing a gas stream through the meter being calibrated during a measured time interval. The quantity of gas that passes through the meter is determined by collecting the gas in a large tank of known volume and measuring its average temperature and pressure, which in turn, reveals the amount of gas.
However, collecting the gas in large tanks—NIST uses a 27 cubic-meter tank (a tank with 27,000 liters capacity)—generates different temperatures in different parts of the tank, which make the average temperature difficult to measure. Those gradients persist for hours or days. Thus, a fast reading is inherently inaccurate.
To get around that problem, current practice entails calibrating many small meters, one at a time, and then using them in parallel to calibrate a larger meter. This is done with a smaller collection tank where temperature differences are reduced to produce more accurate reading. However, the multiple calibrations are inherently time-consuming, and therefore, expensive.
NIST's innovation replaces the difficult problem of accurately measuring the average temperature of a large volume of gas with the easier problem of accurately measuring the average speed-of-sound in the gas.
In one recent, proof-of-concept, paper, NIST researchers deduced the internal shape, thermal expansion and volume of a 300 liter collection tank by measuring which microwave frequencies resonated (formed standing waves) within the evacuated tank.
In a second set of experiments, they filled the tank with argon gas and measured the frequencies of the acoustic resonances. From the frequencies and the pressure, they deduced the mass of the argon in the tank.
Finally, they heated the top of the tank to establish a temperature difference across the gas of 4 percent of the average gas temperature. The temperature difference changed the acoustic resonance frequencies and the pressure; however, the mass of the argon, as deduced from the frequencies and the pressure, was unchanged within 0.01 percent.
This result implies that the acoustic resonance technique could be used to measure the collected gas, even in the presence of a temperature gradient such as those that occur in a much larger tanks located outside the well-controlled environment of a laboratory.
M.R Moldover, J.W. Schmidt, K.A. Gillis, J.B.Mehl and J.D.Wright, Microwave determination of the volume of a pressure vessel. Meas. Sci. Technol. 26, 015304 (2015) doi:10.1088/0957-0233/26/1/015304
K.A. Gillis, J.B. Mehl, J.W. Schmidt, and M.R. Moldover, 'Weighing' a gas with microwave and acoustic resonances. Metrologia 52, pp 337-352 (2015) doi:10.1088/0026-1394/52/2/337