Cybersecurity Insights
a NIST blog
How to deploy machine learning with differential privacy

We are delighted to introduce the final guest authors in our blog series, Nicolas Papernot and Abhradeep Thakurta, research scientists at Google Brain, whose research explores applications of differential privacy to machine learning. - Joseph Near and David Darais
Previous posts in this series have explored differential privacy for traditional data analytics tasks, such as aggregate queries over database tables. What if we want to use state-of-the-art techniques like machine learning? Can we achieve differential privacy for these tasks, too?
Machine learning is increasingly being used for sensitive tasks like medical diagnosis. In this context, we would like to ensure that machine learning algorithms do not memorize sensitive information about the training set, such as the specific medical histories of individual patients. As we’ll see in this post, differentially private machine learning algorithms can be used to quantify and bound leakage of private information from the learner’s training data. In particular, it allows us to prevent memorization and responsibly train models on sensitive data.
Why do we need private machine learning algorithms?
Machine learning algorithms work by studying a lot of data and updating the model’s parameters to encode the relationships in that data. Ideally, we would like the parameters of these machine learning models to encode general patterns (e.g., ‘‘patients who smoke are more likely to have heart disease’’) rather than facts about specific training examples (e.g., “Jane Smith has heart disease”).
Unfortunately, machine learning algorithms do not learn to ignore these specifics by default. If we want to use machine learning to solve an important task, like making a cancer diagnosis model, then when we publish that machine learning model we might also inadvertently reveal information about the training set.
A common misconception is that if a model generalizes (i.e., performs well on the test examples), then it preserves privacy. As mentioned earlier, this is far from being true. One of the main reasons being that generalization is an average case behavior of a model (over the distribution of data samples), whereas privacy must be provided for everyone, including outliers (which may deviate from our distributional assumptions).
Over the years, researchers have proposed various approaches towards protecting privacy in learning algorithms (k-anonymity [SS98], l-diversity [MKG07], m-invariance [XT07], t-closeness [LLV07] etc.). Unfortunately, [GKS08] all these approaches are vulnerable to so-called composition attacks, which use auxiliary information to violate the privacy protection. Famously, this strategy allowed researchers to de-anonymize part of a movie ratings dataset released to participants of the Netflix Prize when the individuals had also shared their movie ratings publicly on the Internet Movie Database (IMDb) [NS08].
Differential privacy helps design better machine learning algorithms
We have seen in previous posts that the noise required to achieve differential privacy can reduce the accuracy of the results. Recent research has shown, counterintuitively, that differential privacy can improve generalization in machine learning algorithms - in other words, differential privacy can make the algorithm work better! [DFH15] formally showed that generalization for any DP learning algorithm comes for free. More concretely, if a DP learning algorithm has good training accuracy, it is guaranteed to have good test accuracy.
This is true because differential privacy itself acts as a very strong form of regularization.
Private Algorithms for Training Deep Learning Models
We now describe two approaches for training deep neural networks with differential privacy. The first, called DP-SGD, adds noise to each gradient computed by SGD to ensure privacy. The second, called Model Agnostic Private Learning, trains many (non-private) models on subsets of the sensitive data and uses a differentially private mechanism to aggregate the results.
DP-SGD
The first approach, due to SCS13, BST14, and ACG16, is named differentially private stochastic gradient descent (DP-SGD). It proposes to modify the model updates computed by the most common optimizer used in deep learning: stochastic gradient descent (SGD).
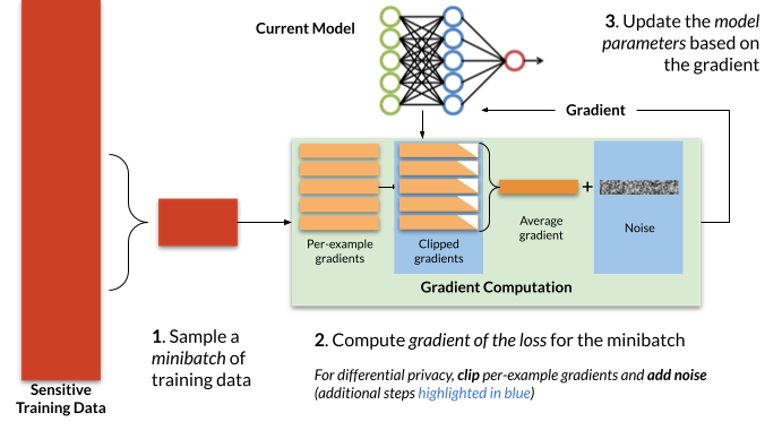
Typically, stochastic gradient descent trains iteratively, repeatedly applying the process depicted in Figure 1. At each iteration, a small number of training examples (a “minibatch”) are sampled from the training set. The optimizer computes the average model error on these examples, and then differentiates this average error with respect to each of the model parameters to obtain a gradient vector. Finally, the model parameters (θt) are updated by subtracting this gradient (∇t) multiplied by a small constant η (the learning rate, which controls how quickly the optimizer updates the model’s parameters).
At a high level, two modifications are made by DP-SGD to obtain differential privacy: gradients, which are computed on a per-example basis (rather than averaged over multiple examples), are first clipped to control their sensitivity, and, second, spherical Gaussian noise bt is added to their sum to obtain the indistinguishability needed for DP. Succinctly, the update step can be written as follows:
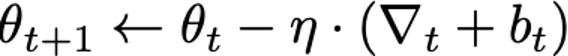
Three main components in the above DP-SGD algorithm that distinguishes itself from traditional SGD are: i) per-example clipping and ii) Gaussian noise addition. In addition, for the analysis to hold, DP-SGD requires that sub-sampling of mini batches is uniform at random from the training data set. While this is not a requirement of DP-SGD per se, in practice many implementations of SGD do not satisfy this requirement and instead analyze different permutations of the data at each epoch of training.
For a fixed DP guarantee, the magnitude of the Gaussian noise that gets added to the gradient updates in each step in DP-SGD is proportional to the number of steps the model is trained for. As a result, it is important to tune the number of training steps for best privacy/utility trade-offs.
For more information on DP-SGD, check out this tutorial, which provides a small code snippet to train a model with DP-SGD.
Model Agnostic Private Learning
DP-SGD adds noise to the gradient during model training, which can hurt accuracy. Can we do better? Model agnostic private learning takes a different approach, and in some cases achieves better accuracy for the same level of privacy when compared to DP-SGD.
Model agnostic private learning leverages the Sample and Aggregate framework [NRS07], a generic method to add differential privacy to a non-private algorithm without caring about the internal workings of it (hence the term, model agnostic). In the context of machine learning, one can state the main idea as follows: Consider a multi-class classification problem. Take the training data, and split into k disjoint subsets of equal size. Train independent models θ1, ..., θk on the disjoint subsets. In order to predict on an test example x, first, compute a private histogram over the set of k predictions θ1(x), ..., θk(x). Then, select and output the bin in the histogram based on the highest count, after adding a small amount of Laplace/Gaussian noise to the counts.
In the context of DP learning, this particular approach was used in two different lines of work: i) PATE [PAE16], and ii) Model agnostic private learning [BTT18]. While the latter focused on obtaining theoretical privacy/utility trade-offs for a class of learning tasks (e.g., agnostic PAC learning), the PATE approach focuses on practical deployment. Both these lines of work make one common observation. If the predictions from θ1(x), ..., θk(x) are fairly consistent, then the privacy cost in terms of DP is very small. Hence, one can run a large number of prediction queries, without violating DP constraints. In the following, we describe the PATE approach in detail.
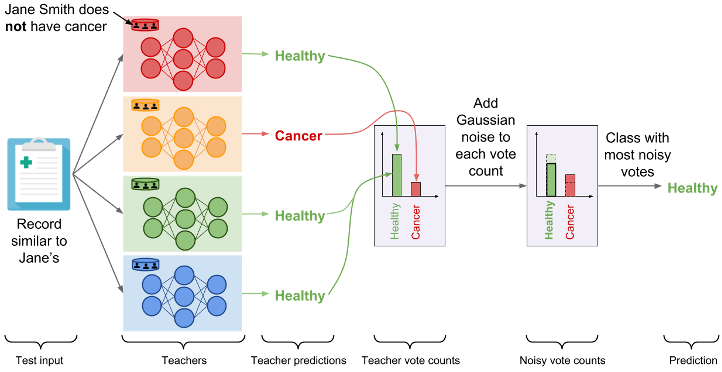
The private aggregation of teacher ensembles (PATE) proposes to have an ensemble of models trained without privacy predict with differential privacy by having these models predict in aggregate rather than revealing their individual predictions. The ensemble of models is obtained by partitioning a private dataset into (non-overlapping) smaller subsets of data. Their predictions are then aggregated using the private histogram approach described above: the label predicted is the one whose noisy count of votes is the largest. The random noise added to vote counts prevents the outcome of aggregation from reflecting the votes of any individual teachers to protect privacy. When consensus is sufficiently strong among the ensemble of models, the noise does not alter the output of the aggregation.
Practical Deployment & Software Tools
The two approaches we introduced have the advantage of being conceptually simple to understand. Fortunately, there also exist several open-source implementations of these approaches. For instance, DP-SGD is implemented in TensorFlow Privacy, Objax, and Opacus. This means that one is able to take an existing TensorFlow, JAX, or PyTorch pipeline for training a machine learning model and replace a non-private optimizer with DP-SGD. An example implementation of PATE is also available in TensorFlow Privacy. So what are the concrete potential obstacles to deploying machine learning with differential privacy?
The first obstacle is the accuracy of privacy-preserving models. Datasets are often sampled from distribution with heavy tails. For instance, in a medical application, there are typically (and fortunately) fewer patients with a given medical condition than patients without that condition. This means that there are fewer training examples for patients with each medical condition to learn from. Because differential privacy prevents us from learning patterns which are not found generally across the training data, it limits our ability to learn from these patients for which we have very few examples of [SPG]. More generally, there is often a trade-off between the accuracy of a model and the strength of the differential privacy guarantee it was trained with: the smaller the privacy budget is, the larger the impact on accuracy typically is. That said, this tension is not always inevitable and there are instances where privacy and accuracy are synergical because differential privacy implies generalization [DFH15] (but not vice versa).
The second obstacle to deploying differentially private machine learning can be the computational overhead. For instance, in DP-SGD one must compute per-example gradients rather than average gradients. This often means that optimizations implemented in machine learning frameworks to exploit matrix algebra supported by underlying hardware accelerators (e.g., GPUs) are harder to take advantage of. In another example, PATE requires that one train multiple models (the teachers) rather than a single model so this can also introduce overhead in the training procedure. Fortunately, this cost is mostly mitigated in recent implementations of private learning algorithms, in particular in Objax and Opacus.
The third obstacle to deploying differential privacy, in machine learning but more generally in any form of data analysis, is the choice of privacy budget. The smaller the budget, the stronger the guarantee is. This means one can compare two analyses and say which one is “more private”. However, this also means that it is unclear what is “small enough” of a privacy budget. This is particularly problematic given that applications of differential privacy to machine learning often require a privacy budget that provides little theoretical guarantees in order to train a model whose accuracy is large enough to warrant a useful deployment. Thus, it may be interesting for practitioners to evaluate the privacy of their machine learning algorithm by attacking it themselves. Whereas the theoretical analysis of an algorithm’s differential privacy guarantees provides a worst-case guarantee limiting how much private information the algorithm can leak against any adversary, implementing a specific attack can be useful to know how successful a particular adversary would be. This helps interpret the theoretical guarantee but should in no way be seen as a substitute for it. Open-source implementations of such attacks are increasingly available: e.g., for membership inference.
Conclusion
In the above, we discussed some of the algorithmic approaches towards differentially private model training which have been effective both in theoretical and practical settings. Since it is a rapidly growing field, we could not cover many important aspects of the research space. Some prominent ones include: i) Choice of the best hyperparameters in the training of DP models: In order to ensure that the overall algorithm preserves differential privacy, one needs to ensure that the choice of hyperparameters itself preserves DP. Recent research has provided algorithms for the same [LT19]. ii) Choice of network architecture: It is not always true that the best known model architectures for non-private model training are indeed the best for training with differential privacy. In particular, we know that the number of model parameters may have adverse effects on the privacy/utility trade-offs [BST14]. Hence, choosing the right model architecture is important for providing a good privacy/utility trade-off [PTS21], and (iii) Training in the federated/distributed setting: In the above exposition, we assumed that the training data lies in a single centralized location. However, in settings like Federated Learning (FL), the data records can be highly distributed, e.g., across various mobile devices. Running DP-SGD or PATE style algorithms in the FL settings raises a series of challenges, but is often facilitated by existing cryptographic primitives as demonstrated in the case of PATE by the CaPC protocol [CDD21], or by distributed private learning algorithms designed specific to FL settings [BKMTT20,KMSTTZ21]. It is an active area of research to address all of the above challenges.
Acknowledgements
The authors would like to thank Peter Kairouz, Brendan McMahan, Ravi Kumar, Thomas Steinke, Andreas Terzis, and Sergei Vassilvitskii for detailed feedback and edit suggestions. Parts of this blog post previously appeared on www.cleverhans.io
Coming Up Next
This post is our last to explore new methods in differential privacy, and nearly concludes our blog series. Stay tuned for a final post where we will summarize the topics covered in this series, wrap up with some final thoughts, and share how we envision this project to live on after the blog.
This post is part of a series on differential privacy. Learn more and browse all the posts published to date on the differential privacy blog series page in NIST’s Privacy Engineering Collaboration Space.

