What is synchrotron radiation?
What is Synchrotron Radiation?
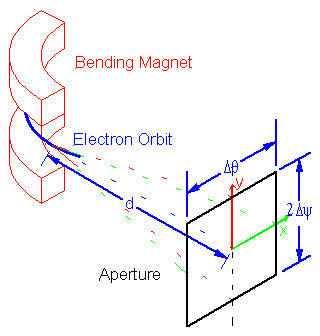
Synchrotron radiation is the electromagnetic radiation emitted when charged particles travel in curved paths. Because in most accelerators the particle trajectories are bent by magnetic fields, synchrotron radiation is also called Magneto-Bremsstrahlung. The emitted spectrum is broadband from the microwave (harmonics of the driving RF field) to x-ray spectral regions. The radiation is vertically collimated and polarized. The synchrotron radiation output can be calculated if the electron energy E, bending radius ρ, electron current IB, angle relative to the orbital plane Ψ0, the distance to the tangent point d and vertical Δψ and horizontal acceptance Δθ angles are known.
Properties of Synchrotron Radiation
Schwinger derived a formalism which allows us to calculate the synchrotron radiation spectrum and other properties like its distribution in space. For SURF, the equation for the radiation power is given by Equation 1.
Equation 1:
$$ P \left(\lambda,\gamma,\psi_0,\Delta\lambda,I_{\rm B},\Delta\psi,\Delta\theta \right)
= \int_{-\psi_0-\Delta\psi}^{+\psi_0+\Delta\psi} \frac{2}{3} \frac{e_0
\Delta\lambda \Delta\theta I_{\rm B} \rho^2}{\varepsilon_0 \beta \lambda^4 \gamma^4}
\left[1 + \left( \gamma \psi \right)^2 \right]^2 \times \left[
K_{2/3}\left[\xi\left(\lambda,\psi \right) \right]^2 + \frac{\left(\gamma
\psi \right)^2}{1+\left(\gamma \psi \right)^2}
K_{1/3}\left[\xi(\lambda,\psi) \right]^2 \right] $$
The radiation power is a function of the wavelength λ, electron energy γ=(E/me c2), angle relative to the orbital plane ψ0, bending radius ρ, horizontal acceptance angle Δθ, the vertical acceptance angle Δψ, and the electron beam current IB. The function ξ is defined by ξ(λ, ψ)2]3/2. Values for the elementary charge e0 and the electric constant ε0 can be found on the NIST Physical Measurement Laboratory Web Site. The functions K1/3[ξ(λ, Ψ)] and K2/3[ξ(λ, Ψ)] are modified Bessel functions of fractional order.
Synchrotron Radiation Spectrum
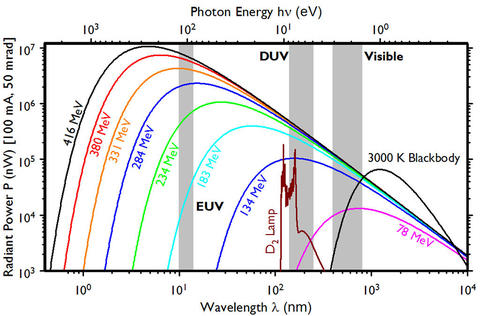
Using Eq. 1 the synchrotron radiation spectrum for SURF can be calculated. Assuming a bandpass of 1% of the wavelength, a horizontal acceptance angle of 50 mrad, a vertical half acceptance angle of 25 mrad, 0 mrad tilt from the orbital plane, a beam current 100 mA, electron energies from 416 MeV to 78 MeV, and an orbital radius of 0.8371 m the output power of SURF is illustrated in figure 2.
Vertical Angular Distribution
The Schwinger equation can be used to calculate the vertical angular spread of synchrotron radiation and its polarization. The radiation power with polarization parallel to the orbital plane is given by Equation 2.
Equation 2:
$$ P_\sigma \left(\lambda,\gamma,\psi,\rho,\Delta\lambda,I_{\rm B},
\Delta\theta\right) = \frac{2}{3} ~ \frac{e_0 \Delta\lambda \Delta\theta I_{\rm B}
\rho^2}{\varepsilon_0 \beta \lambda^4 \gamma^4} \left[1 + \left( \gamma \psi
\right)^2 \right]^2 K_{2/3}\left[\xi\left(\lambda,\psi \right) \right]^2 $$
and the radiation power with polarization perpendicular to the orbital plane is given by Equation 3.
Equation 3:
$$ P_\pi \left(\lambda,\gamma,\psi,\rho,\Delta\lambda,I_{\rm B},\Delta\theta
\right) = \frac{2}{3} ~ \frac{e_0 \Delta\lambda \Delta\theta I_{\rm B}
\rho^2}{\varepsilon_0 \beta \lambda^4 \gamma^4} \left[1 + \left( \gamma \psi
\right)^2 \right] (\gamma\psi)^2 \,
K_{1/3}\left[\xi(\lambda,\gamma)\right]^2 $$
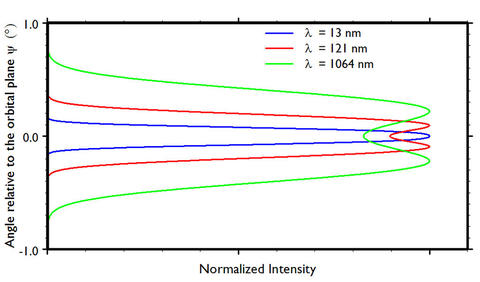
Figure 3 shows to vertical angular spread for the wavelengths 13 nm, 121 nm, and 1064 nm at an electron energy of 380 MeV.