SAT-TMMC: Liquid-vapor coexistence properties - Linear-Force Shifted Potential at 3.5σ
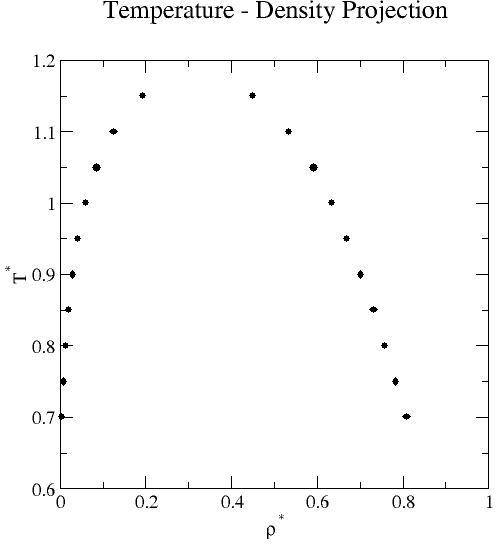
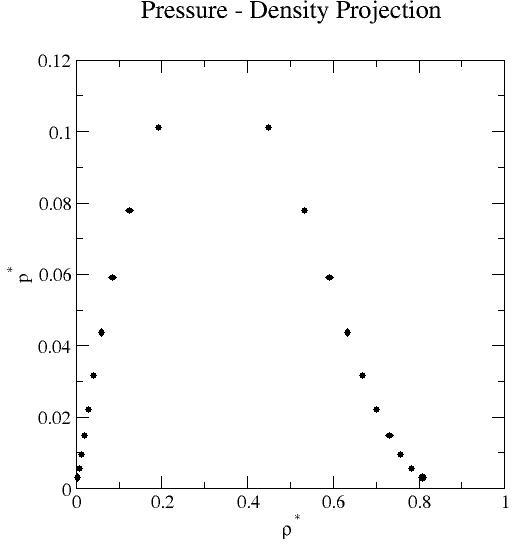
Liquid-vapor coexistence properties obtained by grand-canonical transition-matrix Monte Carlo and histogram re-weighting over the reduced temperature range 0.70 to 1.15 at increments of 0.05. Mean values of the saturation pressure, density, potential energy per molecule, and activity (chemical potential- see below) for each phase are reported.
| METHOD | Grand-canonical transition-matrix Monte Carlo and histogram re-weighting [1, 8-12] |
| V/σ3 | 512 |
| TRUNCATION | Linear Force Shifted at 3.5σ |
| Prob. of Disp. Move | 0.4 |
| Prob. of Ins/Del Move | 0.6 |
| Biasing Function Update Frequency | 1.0E6 trial moves |
| Simulation Length | 4.0E10 trial moves |
T* |
ρvap* |
+/- |
ρliq* |
+/- |
psat* |
+/- |
Uvap* |
+/- |
Uliq* |
+/- |
lnzsat* |
+/- |
| 0.70 | 4.618E-03 | 5.006E-07 | 8.083E-01 | 1.098E-04 | 3.101E-03 | 4.718E-07 | -5.243E-02 | 8.339E-06 | -5.326E+00 | 1.377E-03 | -5.459E+00 | 1.325E-04 |
| 0.75 | 7.959E-03 | 1.227E-06 | 7.840E-01 | 8.368E-05 | 5.600E-03 | 8.326E-04 | -8.520E-02 | 2.301E-05 | -5.129E+00 | 8.304E-04 | -4.957E+00 | 1.130E-04 |
| 0.80 | 1.284E-02 | 1.655E-06 | 7.583E-01 | 5.130E-05 | 9.362E-03 | 9.363E-07 | -1.307E-01 | 3.055E-05 | -4.926E+00 | 1.350E-03 | -4.532E+00 | 5.708E-05 |
| 0.85 | 1.971E-02 | 2.271E-06 | 7.312E-01 | 1.053E-04 | 1.471E-02 | 8.853E-07 | -1.918E-01 | 4.532E-05 | -4.717E+00 | 7.025E-04 | -4.170E+00 | 5.329E-05 |
| 0.90 | 2.913E-02 | 2.558E-06 | 7.018E-01 | 9.298E-05 | 2.199E-02 | 2.079E-06 | -2.724E-01 | 5.178E-05 | -4.498E+00 | 7.970E-04 | -3.859E+00 | 3.804E-05 |
| 0.95 | 4.193E-02 | 4.833E-06 | 6.698E-01 | 7.749E-05 | 3.154E-02 | 1.485E-06 | -3.781E-01 | 7.039E-05 | -4.266E+00 | 6.882E-04 | -3.590E+00 | 1.783E-05 |
| 1.00 | 5.944E-02 | 4.134E-06 | 6.337E-01 | 4.612E-05 | 4.374E-02 | 2.105E-06 | -5.180E-01 | 5.119E-05 | -4.016E+00 | 2.283E-04 | -3.355E+00 | 3.525E-05 |
| 1.05 | 8.425E-02 | 1.060E-05 | 5.911E-01 | 4.367E-05 | 5.901E-02 | 6.162E-06 | -7.107E-01 | 7.238E-05 | -3.733E+00 | 3.994E-04 | -3.105E+00 | 2.686E-05 |
| 1.10 | 1.242E-01 | 3.894E-05 | 5.341E-01 | 6.308E-05 | 7.786E-02 | 3.632E-06 | -1.022E+00 | 3.959E-04 | -3.385E+00 | 5.518E-04 | -2.970E+00 | 2.688E-05 |
| 1.15 | 1.935E-01 | 4.715E-04 | 4.500E-01 | 4.732E-04 | 1.011E-01 | 1.915E-05 | -1.491E+00 | 3.935E-03 | -2.911E+00 | 1.987E-03 | -2.810E+00 | 3.882E-05 |
Remarks:
Uncertainties were obtained from five independent simulations and represent 95% confidence limits based on a standard t statistic. Liquid-vapor coexistence was determined by adjusting the activity such that the pressures of the liquid and vapor phases were equal. Here, the pressure is not the conventional virial pressure [2,3] but is the actual thermodynamic pressure, based on the fact that the absolute free energies can be obtained from the distributions determined from simulation [4]. Alternative methods, for example Gibbs-ensemble Monte Carlo and combination grand-canonical Monte Carlo and histogram re-weighting, can be used to determine liquid-vapor coexistence. A review of standard methods of phase equilibria simulations can be found in Ref. 5.
As introduced in Refs. 2 and 3, the activity, z, is defined as
$$ z = \dfrac{ \exp\left( \beta \mu \right)}{\lambda^3}$$
where Λ is the de Broglie wavelength, β = 1/(kBT) (where kB is Boltzmann's constant), and μ is the chemical potential. It is sometimes more convenient to work with ln z in the simulations and in post-processing. (NOTE: The reported activity is dimensionless, having been scaled by the LJ length cubed.)
Phase-coexistence energies were obtained by determining the mean potential energy at a given value of N for an additional 40 billion MC trials. Combining this information with the particle number probability distribution, the mean potential energy of the coexisting phases can be calculated [6].
For the Lennard-Jones fluid, linear force shifted at 3.5σ, the critical properties were estimated to be Tc*=1.162, ρc*=0.320, and pc*=0.107. Estimates were found via rectilinear diameter analysis of TMMC data computed with V*=512 close to the critical point [7]. (Finite-size scaling analysis has not been completed, so these critical properties should be taken simply as estimates.)
References
- J. R. Errington, J. Chem. Phys. 118, 9915 (2003).
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids (Oxford University Press, New York, 1989).
- D. Frenkel and B. Smit, Understanding Molecular Simulation, 2nd ed. (Academic, San Diego, 2002)., pp.37-38.
- J. R. Errington and A. Z. Panagiotopoulos, J. Chem. Phys., 109, 1093 (1998).
- A. Z. Panagiotopoulos, J. Phys.: Condens. Matter, 12, R25-R52, (2000).
- J. R. Errington and V. K. Shen, J. Chem. Phys., 123, 164103 (2005).
- B. Smit and C. P. Williams, J. Phys.: Condens. Matter, 2, 4281-4288 (1990).
- V. K. Shen and D. W. Siderius, J. Chem. Phys., 140, 244106, 2014.
- V. K. Shen and J. R. Errington, JPC B 108, 19595, 2004.
- V. K. Shen and J. R. Errington, JCP 122, 064508, 2005.
- V. K. Shen, R. D. Mountain, and J. R. Errington, JPC B 111, 6198, 2007.
- D. W. Siderius and V. K. Shen, JPC C 117, 5681, 2013.

