Summary
| For processes involving wetting between two materials, classically defined metrics such as surface or interface energy and contact angle are only a starting point for understanding the dynamic behavior of complex or nanometer-scaled systems that involve chemical reaction/diffusion. The goal of this work is to have a quantitative model of reactive wetting. A good model should allow correct interpretation of dynamic measurements such as the wetting balance (a standard in solderability tests) and the meaning of contact angle measurement of systems not at equilibrium. Tools must also be developed to disseminate these results as codes usable by others. |
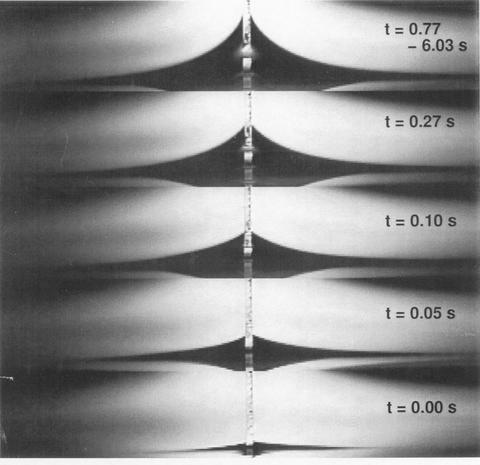 |
Description
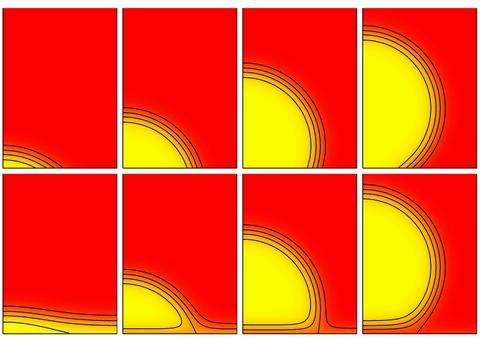
From fundamental physical considerations, we have derived a set of partial differential equations describing wetting and spreading. These equations are derived using a variational thermodynamic principle applied to a two-component alloy system with three (vapor, liquid and solid) phases. The method naturally includes time dependent chemical interactions between substrate and liquid and also non-classical (diffuse interface) effects. (The latter are important for applications where the system size approaches nanometer dimensions).
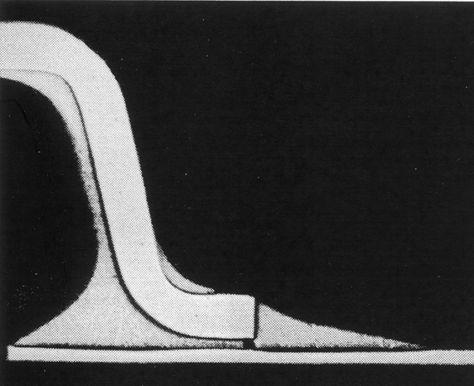 |
Numerical solution of the equations is being performed for specific wetting geometries and parameter values. Results will be compared to predictions of simpler theories and experimental results. The importance of solute transport and its influence on the surface energy will be examined. A sensitivity analysis will determine those factors that dominate in the wetting process. We will use the model to determine how to interpret the measurements of the wetting balance to best aid in the design solder joints for fine-pitch electronics. Subsequently, these tools will be applied to thin film breakup, heterogeneous nucleation on shaped particles and VLS nanowire growth. |
Major Accomplishments
We have implemented a numerical solution scheme to solve these equations and are examining the predictions. Four coupled partial differential equations comprise the model: a mass balance equation, a modified Navier-Stokes equation for the velocity of the matter in the various phases, a modified diffusion equation for the concentration field, and an equation to treat the dynamics of the solid-fluid interface (phase field). Solving this system of coupled equations accurately with appropriate parameters requires sophisticated numerical solution techniques and long simulation times. Our approach thus far has yielded a complete solution of the equations in two dimensions with a slightly nonrealistic parameter set to enable the solution of the equations in a practical time frame. To date we have been able to develop:
1. Methods that suppress unphysical surface flows
2. Relationships between thermodynamic parameters and equilibrium surface energies/contact angles
3. A numerical algorithm that enables large physical parameter differences between phases
4. Methods that stabilize simulations of compressible flow.
The first test of the model will be a comparison to simple experiment in a metallurgical context. One such experiment is the spreading of a liquid metal droplet of tin on a bismuth substrate. Here wetting is accompanied by dissolution of the substrate so that the triple junction motion is governed by solute diffusion as well as capillary processes.
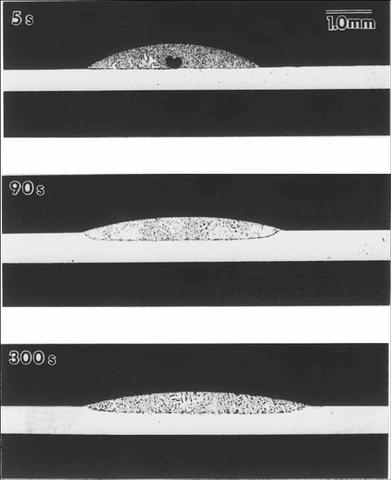
A reactive wetting experiment of liquid Bi-20 wt%Sn spreading on solid Bi.
To date, we cannot match the physical parameters of this experiment in a reasonable computation time, and considerable effort is being devoted to improving our solution methods. However below are shown two time slices from a calculation of the change in shape, composition and accompanying fluid flow pattern when the temperature of a droplet is reduced. The first slice shows the droplet at equilibrium for the high temperature (shown by the black lines). The droplet contracts and dissolves the substrate at a later time and lower temperature. These results show promise for the approach.
|
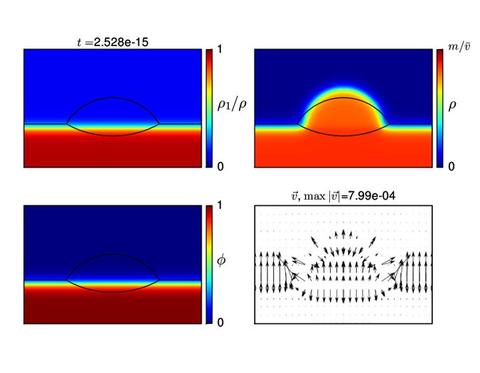 Numerical results obtained for |
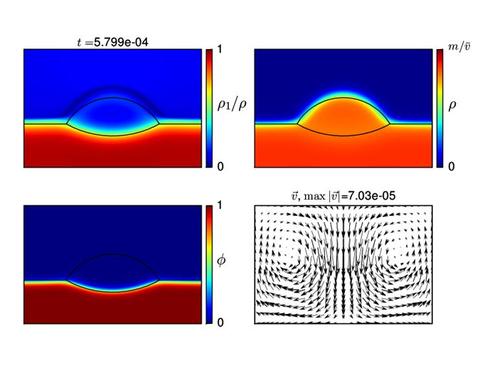 Numerical results obtained for |
Project Summary (PDF)

